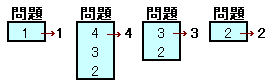
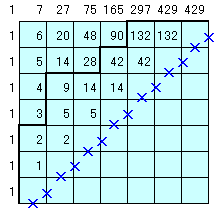
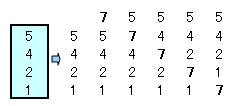第３０８問の解答

問題　［場合の数］

マサルさんはツヨシ君の家庭教師をしています。

マサルさんは、ツヨシ君が帰宅する前に部屋に行き、その日の問題を作りはじめます。問題ノルマは全部で７問で、作成順に１〜７の番号をつけ、台の上に出来た順に重ねて置いていきます。

ツヨシ君は帰宅すると部屋に入り、マサルさんが置いた問題を上から順に解きはじめます。また、ツヨシ君が問題を解いている間もマサルさんは残りの問題を（もしあれば）作り続け、出来るたびに台の上に重ねていきます。

途中の休憩の時点で、ツヨシ君は６番の問題はすでに解いていたそうです。（この時点でも問題は全部完成しているとは限りません。）

では、休憩後にツヨシ君が問題を解く順序は何通り考えられるでしょうか。

解答例１

Nonさん、小杉原　啓さん、ＡЯＯＴさん 、maruhagedonさん、ふじさきたつみさん、Taroさん、CRYING DOLPHINさん、小西孝一さん、M.Hossieさん、ねこやんさん、孫悟空さん、有無相生さん、あさみかずみさん、kokoさん、ステップ　ばい　ステップさん、他　多数

問題の解く順序としては、次のことが成り立ちます。

(補題)ある番号を解いた後に、それより小さい番号が複数残っているときは、大きい順に解くことになる。

（例）１、４、３、２はOK、１、４、２、３はダメ。

参考図１

従って、第６問を解き終わっていることから、残る問題は第７問以外を除いて全て番号の大きい順に解くことになります。
そこで、第７問以外の問題が何問残っているかで場合分けしましょう。

  • ５問残っているとき：残る問題の選び方5C5＝１通り
    　・第７問を既に解いているとき・・・１通り
    　・第７問がまだ残っているとき・・・第７問以外は大きい順だから、第７問の解く順番によって６通り
    合計＝5C5×７通り

同様にして、

  • ４問残っているとき：5C4×６通り

  • ３問残っているとき：5C3×５通り

  • ２問残っているとき：5C2×４通り

  • １問残っているとき：5C1×３通り

  • ０問残っているとき：5C0×１通り（第７問だけ残っている場合）

（第７問以外に４問残っているとき）
参考図２

よって、合計＝5C5×７＋5C4×６＋5C3×５＋5C2×４＋5C1×３＋5C0×１
　＝１×７＋５×６＋１０×５＋１０×４＋５×３＋１×１
　＝１４３通り

答：　１４３通り

以上

解答例２

高橋　道広さん、拓パパさん、他　

  • 第７問を解き終わっているとき：
    　残る５問がいくつ残っているかが決まれば解く順番は番号の大きい順の一通りに決まるので、
    　5C5＋5C4＋5C3＋5C2＋5C1＝２5−１通り（解く問題なしのときを除く）
    　

  • 第７問が残っているとき ：
    　・休憩後、すぐ第７問を解くとき　
    　　残る５問が決まれば解く順番は一通りなので、
    　　5C5＋5C4＋5C3＋5C2＋5C1＝２5通り

　・休憩後、第７問以外の問題をまず解くとき　：
　　最初に解く問題を選ぶのは5C1＝５通り
　　残り４問のうちいくつ残っているか決まれば解く順番は一通りに決まるので、
　　4C4＋4C3＋4C2＋4C1＝２4通り
　　　合計＝５×２4通り

以上から、合計＝２5−１＋２5＋５×２4＝３１＋３２＋８０＝１４３通りになります。

（参考１）

問題が全部でn問あり、第n-1問を解き終わったあとの解く順番（Pnとします）は、上記同様に
　Pn＝２n-2−１＋2n-2＋(n-2)×2n-3＝(n+2)×2n-3−１となります。

解答例１からは、
　Pn＝n-2Cn-2×n＋n-2Cn-3×(n-1)＋・・・＋n-2C1×３＋n-2C0×２−１
となります。

ここで、Ｆn＝nCn×n＋nCn-1×(n-1)＋・・・＋nC1×１＋nC0×０とおくと、
　Ｆn＝nC0×０＋nC1×１＋・・・＋nCn-1×(n-1)＋nCn×n
　　＝nCn×０＋nCn-1×１＋・・・＋nC1×(n-1)＋nC0×n

よって、Ｆn×２＝n×（nCn＋nCn-1＋・・・＋nC1＋nC0）＝（n+1）×２n
 Ｆn＝n×２n-1

従って、
　Pn＝n-2Cn-2×（n-2)＋n-2Cn-3×(n-3)＋・・・＋n-2C1×1＋n-2C0×0
　　　　＋２×（n-2Cn-2＋n-2Cn-1＋・・・＋n-2C1＋n-2C0）−１
　　＝Ｆn-2＋２×２n-2−１
　　＝（n-2)×２n-3＋２×２n-2−１
　　＝（n-2)×２n-3＋４×２n-3−１
　　＝（n＋2)×２n-3−１
となり、解答例２の結果と一致します。

（参考２）

問題が全部でn問ある場合で、第n-1問を解き終わったあとという条件がない場合の解く順番
（Ｋnとします）は、n次のカタラン数となり、Ｋn＝2nCn/(n+1)となります。
　とくに、n=7のときは、Ｋ7＝14C7/８＝４２９通りとなります。

カタラン数については、既に算チャレでも何度か出題されています。

  • 算チャレver.1[248]、[226]、[180]
  • 算チャレver.2[091]
  • 数学の小部屋[006]

下図のようなｎ×ｎの格子上で左下の頂点から右上の頂点へ進む経路との関連を考えます。

  • 問題を作成する⇔格子上で上に進む、

  • 問題を解くことと⇔格子状で

すると、作成した問題数を超えて問題を解くことはありませんから、格子上で対角線よりは左上の経路に限定して進むこととなります。

従って、ちょうどn次のカタラン数になります。

参考図３

上図の経路例では、
　　問題１、２、３を作成→問題３を解く→問題４、５を作成→問題５、４を解く→問題６を作成→問題６を解く
　→問題７を作成→問題７、２、１を解く
となりますので、問題を解く順番だけで言うと、３、５、４、６、７、２、１と対応します。

あるいは、Nonさんが考えられたように、漸化式
　Kn＝Kn-1＋K1×Kn-2＋K2×Kn-3＋・・・＋Kn-2×K1＋Kn-1
からもカタラン数と一致することが得られます。