第３１４問の解答

問題　［場合の数］

ある将棋大会の決勝トーナメント表を作ろうと思います。決勝トーナメント出場者はマサルさん、トモエさん、マサヒコ君、ツヨシ君、サトルさん、ノブユキ君の６人です。

このとき、異なるトーナメント表（*）は何通り作ることができるでしょうか。

(*)異なるトーナメント表とは、見た目だけでなく試合の対戦が異なるものをさします。

解答例１

あんみつさん、Nonさん、CRYING DOLPHINさん、Taroさん、ＩＣさん、Nobさん、Banyanyanさん、小西孝一さん、M.Hossieさん、ふじさきたつみさん、まるケンさん、拓パパさん、POPPYさん、有無相生さん、ステップ　ばい　ステップさん、はっち～さん、トトロ＠Ｎさん、他多数

トーナメント表の形によって場合分けします。
６人の対戦では、対称的なものを除いて下記の６通りになります。

	・A,Bへ配置するのに₆C₂＝15通り・C,Dへ配置するのに₄C₂＝6通り・E,Fは残りの２人が自動的に決まる・このうち、ABとCDの対戦は対称的なので重複よって、15×6÷2＝４５通り		・A,Bへ配置するのに₆C₂＝15通り・C,Dへ配置するのに₄C₂＝6通り・Eへ配置するのに₂C₁＝2通り・Fへは残り1人が自動的に決まるよって、15×6×2＝１８０通り
	・A,Bへ配置するのに₆C₂＝15通り・C,Dへ配置するのに₄C₂＝6通り・Eへ配置するのに₂C₁＝2通り・Fへは残り1人が自動的に決まる・このうち、ABとCDの対戦は対称的なので重複よって、15×6×2÷2＝９０通り		ケース４と同様、15×6×2＝１８０通り
	・Aへ配置するのに₆C₁＝6通り・B,Cへ配置するのに₅C₂＝10通り・D,Eへ配置するのに₃C₂＝3通り・Fへは残り1人が自動的に決まる・このうち、ABCとDEFの対戦は対称的なので重複よって、6×10×3÷2＝９０通り		・A,Bへ配置するのに₆C₂＝15通り・Cへ配置するのに₄C₁＝4通り・Dへ配置するのに₃C₁＝3通り・Eへ配置するのに₂C₁＝2通り・Fへは残り1人が自動的に決まるよって、15×4×3×2＝３６０通り

従って、合計＝４５＋９０＋９０＋１８０＋１８０＋３６０＝９４５通りとなります。

答：　９４５通り

以上

解答例２

マサルさん、高田修成さん、Nonさん、中村明海さん、POPPYさん、kokoさん、他

漸化式で考えます。n人の場合の組み合わせをT_n通りとします。

まず、２人の場合、T₂＝１通り。

次に、n人から(n+1)人に増えるときを考えます。

n人の場合、よく知られたように、試合数＝n-1となります。

従って、あるトーナメントの組み合わせ結果に対し、もう１試合を追加できる場所は、
各試合につき２通りと決勝戦後の１通り＝(n-1)×2+1=2n-1個所。

従って、T_n+1＝T_n×（2n-1）が成り立ちます。

従って、T_n＝（2n-3）×（2n-5）×・・・×3×1となり、
とくに、T_n＝９×７×５×３×１＝９４５通りとなります。

解答例３

高橋　道広さん、Banyanyanさん、ステップ　ばい　ステップさん、Banyanyanさん、トトロ＠Ｎさん、他

まず、トーナメント表数の一般式（S_nとします）を考えます。
ただし、対称的なものも除かずに数えることにします。

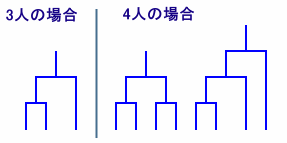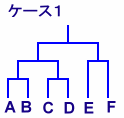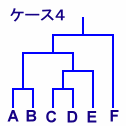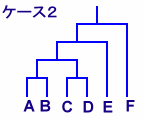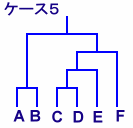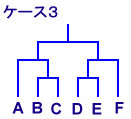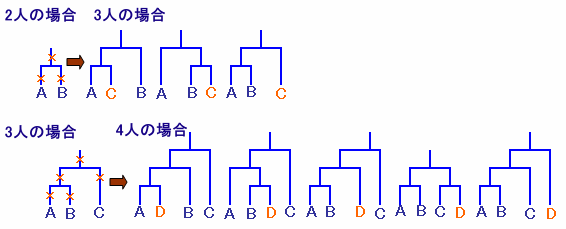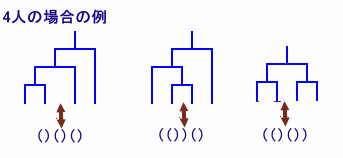
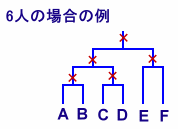
トーナメント表を、カッコでくくったのと考えてみると、n人の場合、試合数は（n-1）なので、
カッコ の個数も（n-1）個となります。

すると、よく知られたように、このときの場合の数は（n-1）次のカタラン数となります。
（算チャレ：248、226、180、算チャレ２：091、数学の小部屋：006）
よって、S_n＝Ｋ_n-1＝_2n-2C_n-1/n

１つのトーナメント表に対し、n人の試合をする場所を決める方法は、n!通りあるので、
　合計でS_n×n!＝_2n-2C_n-1×（n-1）!通りとなります。

これらのうち、各試合の対戦相手は互いに対称的なので２倍に数えていることになります。

従って、重複分を除くと、
T_n＝S_n×n!/２^n-1＝_2n-2C_n-1×（n-1）!/２^n-1＝（2n-2）!/（（n-1）!×（n-1）!）×（n-1）!/２^n-1＝（2n-2）!/（（n-1）!×２^n-1）
　　＝（2n-2）×（2n-3）×（2n-4）×（2n-5）×・・・×２×１／（2n-2）×（2n-4）×・・・×4×2
　　＝（2n-3）×（2n-5）×・・・×３×１
となります。

よって、T_n＝９×７×５×３×１＝９４５通りとなります。

第３１４問の解答

問題 ［場合の数］

解答例１

解答例２

解答例３

問題　［場合の数］