第３７６問の解答

問題［確率（場合の数）］

次のような性質を持つスロットマシンがあります。

  • １回のゲームにつき１枚のコインを賭ける。負ければ賭けたコインは没収され、勝てば２枚のコインがもらえる。（１枚の賭けコインが、２枚に増えるという意味です）

  • また、勝つ確率は１／２である。

このゲームに１枚の持ちコインで挑戦するとき、ちょうど９ゲーム目に持ちコインが無くなる確からしさ（確率）を求めて下さい。

解答例１

あ〜く＠旧Ｎさん、小杉原 啓さん、ねこやんさん、高橋　道広さん、すてっぷさん、小学名探偵さん、 他

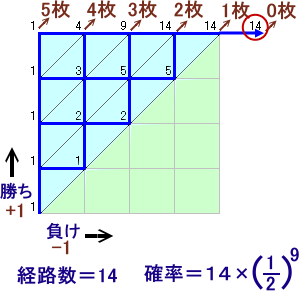
下図のような経路図で考えます。

参考図１

１回ごとのゲームに対し、勝ちのときは上、負けのときは右に進むものとします。

９回のゲームでコイン数がちょうど０になるのは１４通りと求まります。

１回のゲームにつき、勝ち・負けそれぞれ確率は１/２だから、
　求める確率＝１４×（１/２）9＝７/２５６となります。

答：　７/２５６

以上

解答例２

Taroさん、まるケンさん、敬＠Nさん、小西孝一さん、ちこりんさん、 他

題意を満たすのは、８回のゲームで常に勝ち数≧負け数で、最後は勝ち数＝負け数となるような場合の数に等しい。

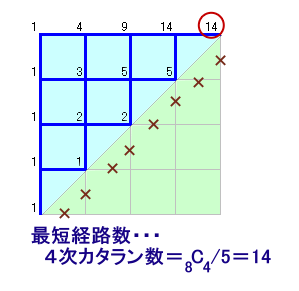
これは、経路図でいえば、４×４の格子上を対角線より右下へは進めないという制限付きで対角点まで進む最短経路数に相当します。

参考図２

これはカタラン数と呼ばれるもので、「算数にチャレンジ！」等ではおなじみのものです。

一般にn次のカタラン数は、Ｋn＝2nCn/(n+1)となります。

本問は４次のカタラン数なので、
　Ｋn＝8C4/５＝１４通り
と求まります。

（参考）- 過去問よりの検索結果 -

  • 算チャレver.1[359]：場合の数：立ち見10席の会場でコンサートが行われます。この席にいる人達はステージの方向(北と西)を向いて鑑賞します。10人とも背が異なるとき,全員が視界をさえぎられずにコンサートを鑑賞することができるような席の割り当て方は何通り？

  • 算チャレver.1[248]：場合の数：あるルール西多賀って、毛布が１０枚、袋が５枚を袋詰めする方法は何通り？

  • 算チャレver.1[226]：場合の数：男７人、女７人を横一列に並べたとき、どこで区切っても左右とも男女の人数が異なるような並べ方はいくつ？

  • 算チャレver.1[180]：場合の数：５０円ショップに５０円玉しかない客と１００円玉しかない客が合計１０人きたとき、硬貨の受け取り方は何通り？

  • 算チャレver.2[091]：場合の数：カタラン数。六角形を対角線で結んで三角形に分割する場合の数は？

  • 数学の小部屋[006]：規則性：正方形半分の格子上を動く最短経路。

    　
    検索に該当する件数は以上 6 件です。

（その他の解法）