問題[場合の数]
|
|
|
|
|
|
縦1列に並べられた8個のイスがあります。 |
|
|
|
|
|
解答例1[イチイチ解法(格子上経路)]
| 浜直君さん、TORAさん、栗原、他 |
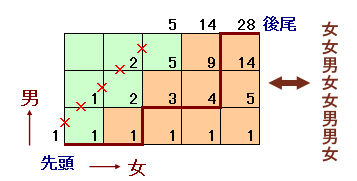
縦3×横5のマス目からなる格子上の経路図で考えます。
左下隅を出発点、右上隅を到着点とする最短経路に対し、
右に進む ⇔ 女が座る
上に進む ⇔ 男が座る
のように対応させれば、男女の座り方と1:1に対応します。
ただし、題意より、45度の対角線より上にある経路は通れません。
(上図の例では、 右右上右右上上 ⇔ 女女男女女男男女)このような経路数の数え方は、
1.出発点の格子上に1を記入
2.通過可能な各格子点について、「左の格子点の数+下の格子点の数」を記入
としていくと、到着点の記入数が求める最短経路数となります。このルールに従って計算すると、到着点の記入数は28となるので、最短経路数は28、
よって、求める男女の座り方も、28通りと求まります。答 28通り
以上
(参考)カタラン数に関する過去問
解答例2[35-7]
| mhayashiさん、明菜さん、他 |
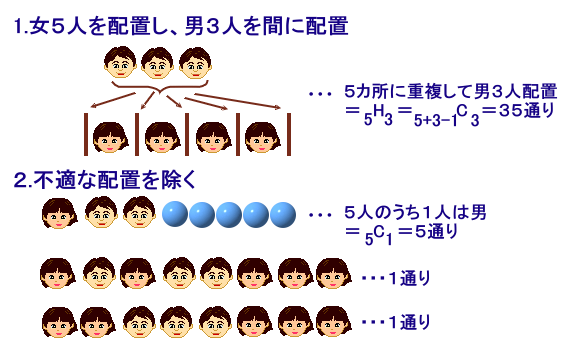
1.最初に女5人を配置し、その間の5カ所に重複を許して男3人を配置してみます
・・・ 5H3=5+3-1C3=7C3=35通り2.上記より題意に不適な配置を除きます
(ア)女男男○○○○○ ・・・ ○5人のうち、1人は男=5C1=5通り
(イ)女男女男男女女女 ・・・ 1通り
(ウ)女女男男男女女女 ・・・ 1通り
従って、求める男女の座り方は、
35−(5+1+1)=28通り
と求まります。
解答例3[最初の4番目までの考察]
| ゴンともさん、始 受験勉強君さん、 他 |
1.最初に4人がすべて女の場合
・・・ 残り4人のうち1人は女=4C1=4通り2.最初の4人のうち、3人が女の場合
女女女男○○○○、女女男女○○○○、女男女女○○○○の3通り
・・・ 残り4人のうち2人は女=4C2=6通り
合計=3×6=18通り3.最初の4人のうち、2人が女の場合、5人目は女でなければならない
女男女男女○○○、女女男男女○○○の2通り
・・・ 残り3人のうち1人は女=3C1=3通り
合計=2×3=6通り従って、求める男女の座り方は、
4+18+6=28通り
と求まります。
(その他の解法)
- 地道に書く ・・・ふうきさん、うめこさん、R.Tさん、tymさん、kasamaさん、 まるケンさん、tomhさん、かわせみ太さん、kobaさん、 他