このページでは、「もうひとつの算数チャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
42問、41問、40問、39問、38問、37問、36問、35問、34問、33問
第42問:
成田空港で1998人の人に、ワールドカップで日本と韓国が予選突破できるかどうかを予想してもらいました。
- 「日本が予選突破する」と答えたのは、男女同じ人数でした。
- 男の人の回答では60%の人が「日本が予選突破」と答え、「韓国が予選突破」と答えたのは3人に1人でした。
また、男の人の回答で「日本だけ」は「韓国だけ」の9倍でした。- 女の人の回答では75%の人が「日本が予選突破」と答え、「韓国が予選突破」と答えたのは4人に1人でした。
また、この中で「韓国だけ」は15人でした。さて、「日本も韓国も予選敗退」と答えたのは、全部で何人でしょう?
ヒント1:
まず、男女比率を求めて下さい。
第41問:
連続した27個の整数があります。 この27個を「偶数のグループ」と「奇数のグループ」に分け、それぞれのグループに含まれた整数の合計を比べてみたところ、その差が74でした。
では、この27個の整数の和はいくらでしょうか。
ヒント1:
1、2番目の数、3、4番目の数・・・とペアにして考えると? 参考図1ヒント2:
それぞれのグループで、整数の平均値はいくら? 参考図2
第40問:
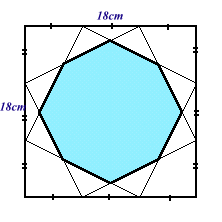 |
ヒント1: ヒント2: |
第39問:
|
ヒント: 同じ人に投票した人が6人いるかな? 参考図 |
第38問:
|
ヒント: 1円から20円までの税抜き価格に対して、消費税はどうなるのかな? 参考図 |
第37問:
|
ヒント: ○○○×9=○○○2だから、一の位の数○はいくらかな? |
第36問:
問題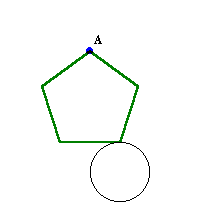 |
ヒント1: ヒント2: |
第35問:
あるモンスターは戦闘の際、毎分一定量のエネルギーを放出しますが、その一方でこれを一定量だけ補充しながら戦い、エネルギーが無くなれば戦えなくなります。
エネルギー放出量を通常より10%増、補充量を10%減なら60分でスタミナ切れ、
放出量10%減、補充量10%増なら90分戦えます。
では、放出量・補充量ともに10%減の場合、通常と比べて戦える時間はどうなるのか?ヒント1:戦える時間数は、放出量と補充量の差と比例する。
ヒント2:参考図
エネルギー放出量を通常より10%増、補充量を10%減のときと、
放出量10%減、補充量10%増の場合の平均をとるとどうなる?ヒント3:参考図
放出量・補充量ともに10%減の場合、通常と放出量と補充量の差はどうなるのかな?
解答のページへ:
第34問:
問題:
ある整数に対して、それが偶数の場合は2で割り、奇数ならば1を足します。
そして、この操作を結果が1になるまで続けます。
例えば6は、6→3→4→2→1と4回の操作で1になります。
10回の操作で1になる整数は全部で55個あり、
その中の21個が奇数であることが分かっています。(注1)
では、12回の操作で1になる整数は全部で何個ありますか。ヒント1:
1回の操作で、
結果が偶数:(例)3→4(奇数→偶数)、8→4(偶数→偶数)の2とおり、
結果が奇数:(例)6→3(偶数→奇数)の1とおりがある。
では、2回の操作では?ヒント2:
n回の操作で1になる偶数の個数をan、奇数の個数をbn、合計をcnとおくと、
an、bn、cnやan+1、bn+1、cn+1等には、どんな関係があるのかな?解答のページへ:
第33問:
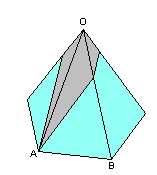 |
|
ヒント1:
立体の形を見てみましょう。 全体図、平面図、立面図、側面図
ヒント2:展開図