このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
112回、111回、 110回、109回、108回、107回 、106回、105回、104回、103回
第112回:
問題:
|
ヒント1: 一つのものを買うときの値段は、貨幣価値に逆比例し、同じ通貨枚数で買えるものの個数は、貨幣価値に比例するよ。 ヒント2:面積で考えてみたら? 参考図 解答のページへ: |
第111回:
問題:
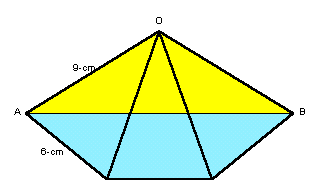 |
ヒント1: 元の2等辺三角形と相似な三角形がいくつあるかな? 参考図1 ヒント2: 解答のページへ: |
第110回:
問題:
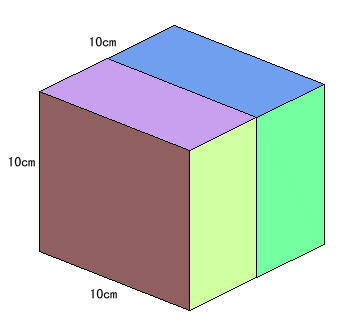 |
ヒント1: 一回切ると、立体の表面積はどれだけ増えるかな? 参考図1 ヒント2: 解答のページへ: |
第109回:
問題:
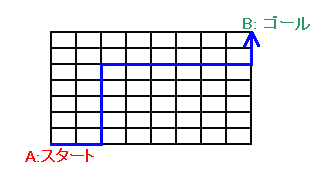 |
ヒント1: 2度目に曲がり角は、どこにくるかな? 参考図1 ヒント2: 右に進むのをE、上に進むのをNというように表すと、EとNの並び方はどうなるかな? 参考図2 解答のページへ: |
第108回:
問題:
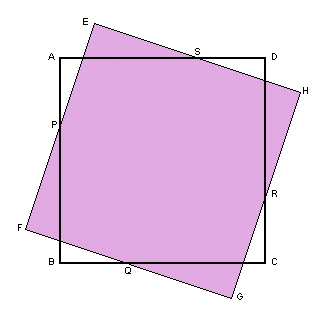 |
ヒント1: 点P、点Q、点R、点Sを結んで出来る四角形PQRSはどんな四角形かな? 参考図1 ヒント2: △APSと正方形ABCDの面積比は? 解答のページへ: |
第107回:
問題:
| ある中学校の本年度の入試は、受験者数は52%、合格者数は10%、不合格者数は60%、昨年度よりも増えました。 また、本年度の合格者の平均点は合格基準点よりも24点高く、不合格者の平均点は合格基準点よりも14点低かったそうです。 また、全受験者の平均点は216.4点でした。 では、本年度、この中学校の合格基準点は何点だったでしょうか。 |
ヒント1:
今年度の不合格者数と、仮に増加率が合格者と同じ10%としたときとの差はどうなるでしょう? 参考図1
ヒント2:
今年度の不合格者数、合格者数が分かったら、全体の平均点は不合格者の平均、合格者の平均とどんな関係でしょうか?
不合格者の平均を仮に0とすると計算しやすいよ。 参考図2
解答のページへ:
第106回:
問題:
| マサル君、トモエさん、ツヨシ君の3人が、上りのエスカレーターに同時に乗りました。 トモエさんはじっとしていましたが、マサル君とツヨシ君はエスカレーター上で歩きました。 また、マサル君がこの上りエスカレーターを上の階から歩いて下りると、72段歩いたところで下の階に着くそうです。 マサル君は、ツヨシ君の2倍の速さで上り下りできます。 では、この上りエスカレーターは全部で何段あったでしょうか。 |
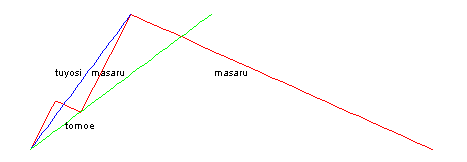 ヒント1:
ヒント1:
マサル君がエスカレータを上り下りしたときの時間は?参考図1
ヒント2:
エスカレータが止まっていると考えたら?参考図2
解答のページへ:
第105回:
問題:∠BAD=40°、∠DAC=70°、AD=6cm、BD:DC=5:4である。ABの長さはいくらか。
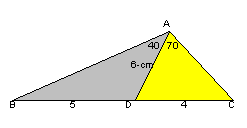 ヒント1:
ヒント1:
頂点Cから直線を辺DAに平行となるように引く。参考図1
ヒント2:
BAの延長線上に点FをAF=6cmとなるようにとる。参考図2
ヒント3:
DをとおりBAに平行に直線を引く。参考図3
ヒント4:
三角関数を用いて、△ABCと△ADCの面積を求める。
解答のページへ:
第104回:
下図のD.B2の長さを求めよ。
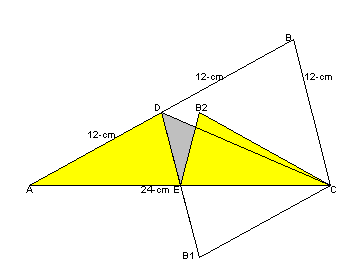
問題:
AB=AC=24cm、BC=12cm、DはABの中点である。
DCを折り目に折り返し、さらにECを折り目に折り返して移動したBの点をB1、B2とする。
D.B2の長さはいくらか。
ヒント1:
EはACの中点になる。参考図
解答のページへ:
第103回:
下図の展開図から得られる立体の体積を求めよ。
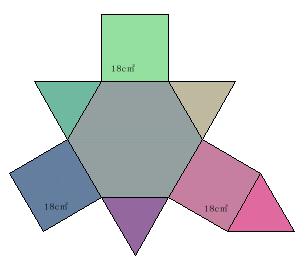 問題:
問題:
下図の展開図から得られる立体の体積を求めよ。
ヒント1:
ヒント2:
この立体の底面である正6角形は、ある立方体を2つに切断して出来ます。切断図
解答のページへ: