このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
第182回、第181回、第180回、第179回、第178回、第177回、第176回、第175回、第174回、第173回
第182回:
| 1から1000までの数字があります。これを上図のように3通りの方法で番号を付けました。
(A)1番から1000番まで順番に番号を付ける。 |
ヒント:数字が8個、または7個で数えるということは? 参考図1 参考図2 解答のページへ
第181回:
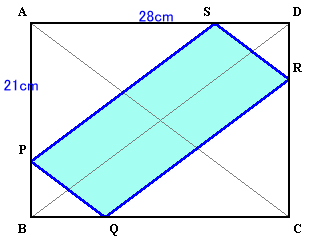 |
参考図1 解答のページへ |
第180回:
| マサルさんの経営する店は、1個50円の商品だけを売っている「50円ショップ」です。 ある朝、開店してみると、50円玉が1枚もないことに気づきました。これではおつりを出すことが出来ません。 結局この日は、50円玉しか持っていない人と100円玉しか持っていない人が同数だけ来たのですが、うまい具合にお客さんが来てくれたので、100円玉しか持っていない人に「おつりがないからお断り」はしないで済んだそうです。 このとき、例えば全部で4人のお客さんが来店したとすると、マサルさんの硬貨の受け取り方は、 A.50円玉→ 50円玉→100円玉→100円玉 B.50円玉→100円玉→ 50円玉→100円玉 の2通りが考えられますね。 さて、全部で10人のお客さんが来たとすると、マサルさんの硬貨の受け取り方は何通り考えられるでしょうか。 注・・・1人のお客さんは1個の商品だけを買うものとします。また、50円玉、100円玉以外の硬貨・紙幣は全く持ってないものとします。 |
ヒント:最短経路の問題で考えてみましょう。 参考図1 解答のページへ
第179回:
| ある長距離徒歩大会に出場したマサル君、トモエさん、ツヨシ君は、 それぞれ毎時3km、毎時4km、毎時5kmで歩くことにしました。 この大会では、コース脇に「あと○km」という標識がスタートから1kmごとに表示されています。 それを見ながら歩いていたマサル君は、 「あ、スタートからの経過時間(単位:時間)と残りの距離が同じだ....。」 とあるときに思ったそうです。 また、トモエさん、ツヨシ君もそれぞれ同じこと道中に思ったそうです。 さて、この大会は、全長何kmの距離を歩くことになっていたのでしょうか。 考えられる距離の中で最短のものを答えてください。 |
ヒント:経過時間と残り距離が同じになるのはどんなときでしょう。 参考図1 解答のページへ
第178回:
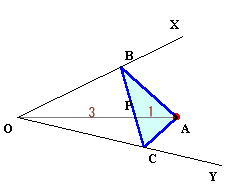 |
|
ヒント:三角形ABCの周の長さが最小になるのはどんなときでしょう。 参考図1 参考図2 解答のページへ
第177回:
| 2つの整数A、Bがあります。この2つの整数をもとに、 A+B=C B+C=D C+D=E ・・・ L+M=N と、Nまで順に求めました。 ここで、AからNまでの和を求めると、5307となったそうです。 このとき、Iはいくつでしょうか。 |
ヒント:A、B、C、・・・は、どんな数列になるでしょう。 参考図 解答のページへ
第176回:
図1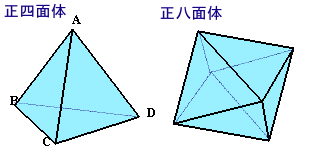 |
図2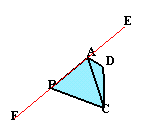 |
| (1) 一辺の長さが2cmの正四面体は、一辺の長さが1cmの正四面体(ア)個と、一辺の長さが1cmの正八面体(イ)個でできています。ア、イに当てはまる整数を答えてください。
(2) さて、正四面体ABCDの全ての辺をそれぞれ両方向に2倍ずつ伸ばすと、全部で12個の点ができます。これらの12個の点を頂点とする立体(凸多角形)の体積は、もとの正四面体の体積の何倍でしょうか。 |
ヒント:まず、どんな立体になるか考えてみましょう 参考図1 参考図2
解答のページ(設問1 設問2)へ
第175回:
| マサル君が、高さ4.8mの街灯Aから7mの距離のところに立ったところ、“ある長さ”の影ができました。 次にマサル君が、高さ4mの街灯Bから8mの距離のところに立ったところ、“ある長さ”の1.5倍の長さの影が出来たそうです。 さて、マサル君の身長は何cmと考えられるでしょうか。 |
第174回:
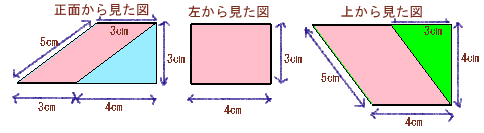
| 上の図は、すべての面が平面になっている立体図形の、正面(前)から見た図、左から見た図、真上から見た図を描いたものです。 では、この立体の体積は何cm3でしょうか。 |
ヒント:どんな立体になるでしょう 参考図1 参考図2 解答のページへ
第173回:
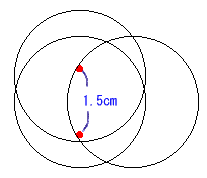 |
|
[Next]