「算数にチャレンジ」にチャレンジ！#７

　このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。

第１７２回、第１７１回、１７０回、１６９回、１６８回、１６７回、１６６回、１６５回、１６４回、１６３回

第１７２回：

　　あるデパートの２Ｆから３Ｆに向かう上りエスカレーターで、マサルさんとトモエさんが遊んでいました。

　あるとき、トモエさんが２Ｆから３Ｆへ、マサルさんが３Ｆから２Ｆへ同時に歩き始めました。トモエさんは３Ｆに着くとすぐに２Ｆに向かって、マサルさんは２Ｆに着くとすぐに３Ｆに向かって歩き始めます。このとき、マサルさんが１度目にトモエさんに出会ってから２度目に出会うまでに下り方向には６０歩、上り方向には１５歩だけ歩いたそうです。

　さて、今度はマサルさんが３Ｆから２Ｆに向かって歩き、トモエさんは２Ｆから買い物カゴをエスカレーターに乗せて（置いて）３Ｆに向かわせる遊びをしました。このとき、

（１）　マサルさんは２Ｆから数えて何段目の地点で買い物カゴと出会ったでしょうか。
（２）　マサルさんは買い物カゴを受け取るまでに何歩歩いたでしょうか。

　ただし、２人の歩くペースは同じものとします。

ヒント：速度比のを考えてみましょう　　参考図１　　参考図２　　解答のページへ

第１７１回：

問題図

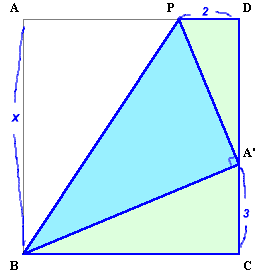
　上の図は、長方形ＡＢＣＤの頂点Ａが、辺ＤＣ上にくるようにＰＢを折り目として折ったところを示しています。

　では、ＣＡ’＝３cm、ＤＰ＝２cmのとき、ＡＢの長さは何cmでしょうか。

ヒント：三角形の相似を考えてみましょう　　参考図　　解答のページへ

第１７０回：

　あるクラスで、カードを使ったゲームをしました。

　まず、クラス人数の２倍の枚数のカードを用意し、１から順に通し番号を記入しました。次に、生徒たちに２枚ずつカードを配ります。

　生徒は、受け取った２枚のカードの番号の差を自分の得点とします。例えば、１４番と２３番のカードを受け取ったなら、得点は２３－１４＝９点となります。

このとき、全員の得点の和は、最も大きいときで４００点になります。

　では、全員の得点の和は、全部で何通り考えられるでしょうか。

ヒント：最小得点から最大得点をとるケースを考えてみましょう　　参考図１　参考図２
　解答のページへ

第１６９回：

　上の図のように、２種類（ｘcm、ｙcm）の竹ひごを使って立体を作りました。この立体は、前・後・右・左のどちらから見ても十字形に見えるそうです。この立体に紙で面を付けたところ、表面積が２８８cm²でした。

　では、この立体の体積は何cm³でしょうか。ただし、竹ひごの長さは２種類ともcmの単位で整数であるものとします。

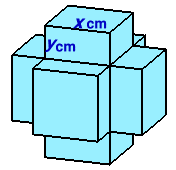ヒント：ｘとｙの関係を求めてみましょう　　　解答のページへ

第１６８回：

　面積が１８cm²である正方形が６枚と、正方形と一辺の長さが等しい正六角形が８枚あり、この１４枚を面とする多面体（１４面体ですね）をつくります。

　このとき、完成した多面体の体積を求めてください。

ヒント：立体の形を考えてみましょう　　参考図１　　　解答のページへ

第１６７回：

　　左図左のような、ＯＰ＝５cmの円すいがあります。

　この円すいに、左図右のようなＡＢ＝ＡＣ＝５cm、ＢＣ＝８cmの二等辺三角形の紙を巻きつけることにしました。円すいの母線であるＯＰとＡＢが重なるようにして巻きはじめたところ、二等辺三角形はこの円すいを２周しました。そして、点Ｃはちょうど点Ｐ（二等辺三角形でいえばＢ）と重なったそうです。

　では、この円すいの側面上で、二等辺三角形の紙が２重に巻かれている部分の面積は何cm2でしょうか。

ヒント：展開図を考えてみましょう　　
　参考図１　　参考図２　解答のページへ

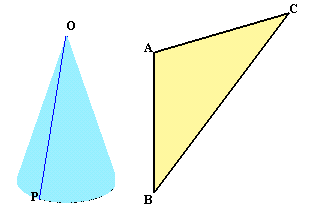第１６６回：

　１２３３個のおはじきと、２２９５個のベーゴマ、２９９９枚のメンコがあります。

　これらを、集まっている子どもたちに同じ数ずつ、できるだけ多く配ることにしました。すると、ベーゴ
マはおはじきよりも１２個多く余ってしまいました。また、メンコはおはじきの３倍も余ってしまったそう
です。

　では、集まっている子どもの人数は何人だったと考えられるでしょうか。考えられるだけ答えてくださ
い。

ヒント：余りの関係から、人数は？？の約数となるはず　　　解答のページへ

第１６５回：

　左図のに、四角形ＡＢＣＤの頂点Ａと頂点Ｃ、頂点Ｂと頂点Ｄを結び、それぞれの中点Ｎ、Ｍを取りました。また、ＡＣとＢＤの交点をＰとします。

　四角形ＡＢＣＤの面積は８０cm²、三角形ＡＭＣの面積は２０cm²、三角形ＢＮＤの面積は１２cm²となっています。

　このとき、三角形ＰＢＣの面積を求めてください。

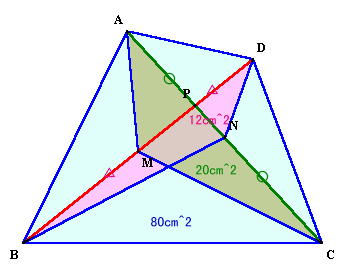ヒント：面積比と辺の比を考えてみましょう　
　　解答のページへ

第１６４回：

　左図のような「たこ型」と言われるＡＢ＝ＡＤ、ＢＣ＝ＤＣの四角形があります。また、∠ＡＢＣ＝∠ＡＤＣ＝９０°です。
　この四角形の、ＡＣとＤＢの交点をＰとすると、ＡＰ＝５０cm、ＰＣ＝８cmでした。
　さて、この四角形に３本の折り目をつけて折って、四面体を作ります。このとき、四面体は２種類つくることができます。

では、この２種類の四面体の体積比を求めてください。

ヒント：折り目の付け方を考えてみましょう　　
　参考図１　　参考図２　解答のページへ

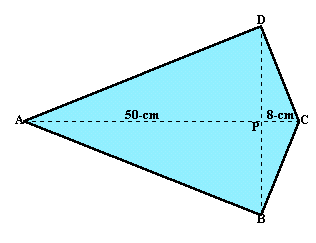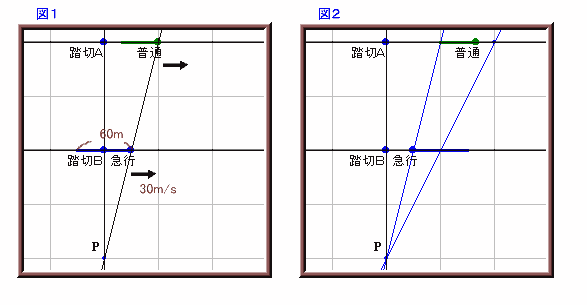
第１６３回：

　平行に伸びる２本の線路上を、普通列車と急行列車が走っています。
　いまマサルさんは、Ｐ地点に立っていて、踏切Ａ～踏切Ｂの距離と踏切Ｂ～Ｐ地点の距離は等しいそうです。

　図１は、急行列車が普通列車を追い越すところを示しています。マサルさんが、「完全に急行列車しか見えない時間」を測ったところ、２秒だったそうです。
　図２は、急行列車と普通列車がすれ違うところを示しています。追い越すときと同様に、「完全に急行列車しか見えない時間」を測ったところ、１秒だったそうです。
　また、急行列車の速度は毎秒３０ｍで、長さは６０ｍであることが分かっています。

（１）　普通列車の速さは毎秒何ｍでしょうか。
（２）　普通列車の長さは何ｍでしょうか。

ヒント：両方の列車の端っこが重なったときの図を考えてみましょう　　　参考図１　　　解答のページへ