このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
162回、161回、160回、159回、158回、157回、156回、155回、154回、153回
第162回:
 |
|
第161回:
 |
|
第160回:
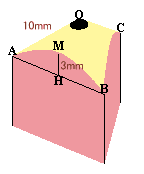
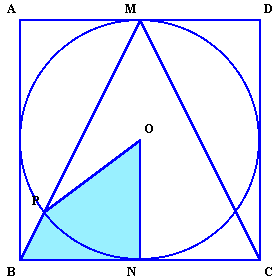
| 上の図1のような竹ひごを使って、図2のような台形を作ったところ、面積が14cm2となりました。 竹ひご5本を使って図3のような正5角すいを作りました。このとき、側面の二等辺三角形の頂角は36゜でした。 (1)この正5角すいの表面積を求めてください。 (2)図4−Aは、図3の正5角すいを2つ組み合わせて作った10面体です。 このとき、図4−Aの立体と、図4−Bの立体の表面積の合計を求めてください。 |
ヒント:正5角錐の展開図と図2を適当に分割してみましょう 参考図1 参考図2 解答のページへ
第159回:
| ある4ケタの整数 A49B があります。 この整数を、2ケタの整数 CD で割ったところ、ちょうど割り切れて商は49になったそうです。 では、A、B、C、Dに当てはまる数をそれぞれ求めてください。 |
ヒント:1001は7の倍数です。 解答のページへ
第158回:
 |
|
第157回:
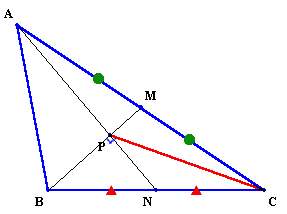 |
|
第156回:
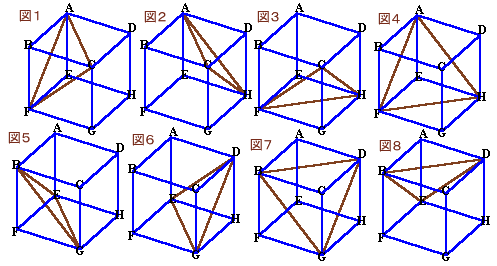
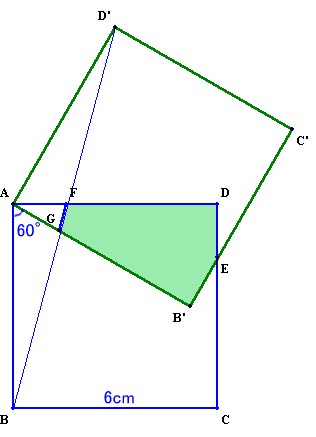
| 一辺の長さが5cmの立方体があります。 この立方体を、上の図のような方法で8回切断します。 このとき、8回の切断が終わるまで立方体は動かしません。つまり、8回の切断が終了するまでは、この立体は立方体の形を保っており、切断が終了するとバラバラになるというわけです。 さて、この作業後にできた、たくさんの小さな立体のうち最も体積が大きい立体は何cm3でしょうか。 |
ヒント:どんな立体になるでしょう? 参考図1 参考図2 解答のページへ
第155回:
| マサルさんとトモエさんが、コインを使ってゲームをしました。じゃんけんをして、勝った方は、負けた方の持っているコインの半分をもらえるというゲームです。 最初、2人とも64枚ずつ持ち、6回勝負したところ、マサルさんのコインは79枚になったそうです。(引き分けはありませんでした) では、マサルさんから見て、2人の勝負はどのような結果だったのでしょうか。 「勝ちを1、負けを0」として、例えば、「勝ち−負け−負け−負け−勝ち−勝ち」ならば、「100011」と答えてください。 |
第154回:
| 1周6300mの池があります。この池の周りにクイを打つとき、次のようにしました。 まず、スタート地点から1mの地点にクイを打ちます。(スタート地点には打ちません) 次に、そこから3m進んだ地点(つまりスタート地点から4m進んだ地点ですね)にクイを打ちます。その後、5m進んだ地点、7m進んだ地点、・・・と次々にクイを打っていきます。 何周かして、スタート地点にクイを打ったところでやめることにします。 このとき、クイは何本打つことになるでしょうか。 ※・・・ただし、スタート地点以外では同じ所に2ヶ所以上クイを打っても良いものとします。 |
ヒント:クイをn本打つとしましょう。 参考図 解答のページへ
第153回:
| 次のようなゲームをしました。 1.マサル君がサイコロを2回ふる。このとき、大きいほうの出目をA、小さい方の出目をBとして覚えておく。(同じ出目なら、AとBは同じ数になります) 2.マサル君はA−Bの計算結果をW君に、A÷Bの計算結果から(もし小数になったら)小数を切り捨てた数をYさんに教える。(※) その後、W君とYさんの間では次のような会話がかわされました。 W君 「ん〜、差だけじゃ分からないな〜」 Yさん「差をしってるW君が分からないのね。えっと....でも私も分からないわ。」 W君 「A÷Bの整数の部分を知ってるYさんも分からないということは..... そうか、分かった!」 Yさん「あ、W君が分かったのなら、私も分かったわ。」 さて、サイコロをふって出たA、Bの数はそれぞれいくつだったでしょうか。 ※・・・このお二人はすご〜〜く賢いことで知られています。(^^;;。 |
ヒント:A,Bの考えられる組み合わせのときにW、Yはどうなるでしょう?
参考図 解答のページへ