第300問、第299問、第298問、第297問、第296問、第295問、第294問、第293問、第292問、第291問
 |
|
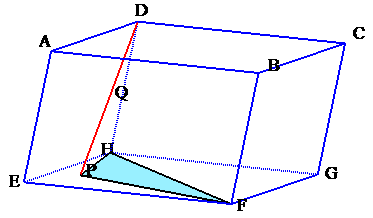
左図のような各面が平行四辺形からなる平行六面体ABCD-EFGHがあります。 今、底面上の点Pを△EFHの内部にとり、DP上の点Qをとったとき、次の関係が成り立ちました。
では、△PFHの面積は何cm2でしょうか。 |
|
ヒント:体積比を面積比に? 参考図1 参考図2 解答のページへ
|
マサルさんは、あるデパートの下りエスカレータに乗って歩いています。
途中、マサルさんは財布を落としてしまいましたが、それに気づいたのは財布を落としてから15段歩いたところで、そこは下の階まで残り18段の地点でした。
マサルさんは財布を落としたのに気づくとすぐに方向転換し、歩いてエスカレータを上りはじめました。その後マサルさんは財布を拾うと下に向かって歩き始め、財布を拾ってから21段歩いたところで下の階に着いたそうです。
では、マサルさんが下の階から、下りエスカレータを財布を落とした地点まで歩いて上るとすると、何段歩いたところで到着するでしょうか。
なお、マサルさんはエスカレータをのぼるときも下るときも同じペースで歩を進めるものとします。 |
ヒント:速度比は? 参考図1 参考図2 解答のページへ
 |
|
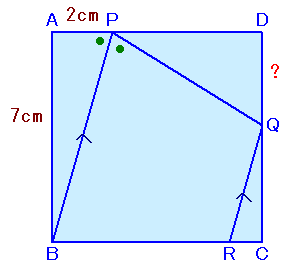
左図のような、一辺の長さが7cmの正方形ABCDがあります。
点Pを辺AD上にAP=2cmとなる位置に、点Qを辺CD上に∠APB=∠QPBとなるようにします。
また、点Qを通りBPに平行な直線と辺BCとの交点をRとします。
このとき、DQの長さは何cmでしょうか。 |
ヒント:相似に着目? 参考図1 解答のページへ |
 |
|
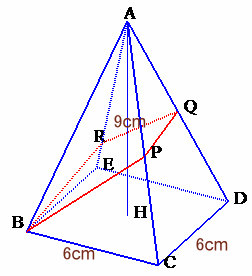
左図のような、底面が一辺6cmの正方形、高さが9cmで、側面がすべて合同な二等辺三角形でできた正四角錐A−BCDEがあります。
まず、この正四角錐を平面ABD、平面ACEで切断し、次に、この正四角錐を図のような平面BPQRで切断します。このとき、AQ:QD=1:1となっています。
その結果、正四角錐は8つの立体に分割されますが、その中から形が三角錐(四面体)であるもの4つの体積を測ったところ、その比は2:3:4:6でした。
では、上図の正四角錐A−BPQRの体積は何cm3でしょうか。 |
ヒント:相似に着目? 参考図1 参考図2 解答のページへ
|
|
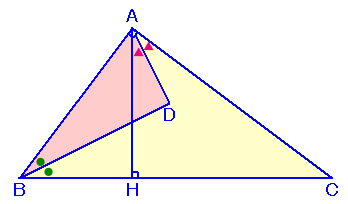
上の図のような∠A=90゜の直角三角形ABCがあり、頂点Aから辺BCに降ろした垂線の足をHとします。
また、△ABHの周の長さが36cm、△AHCの周の長さが48cmとなっています。
いま、∠Bの二等分線と∠HACの二等分線の交点をDとします。
このとき、△ABDの面積を求めてください。 |
ヒント:相似に着目? 参考図1 参考図2 解答のページへ
|
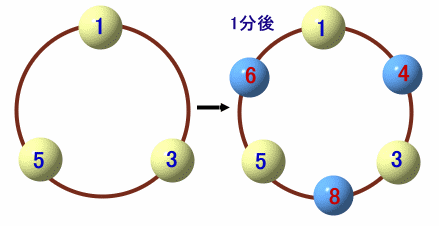
上の図のように、円周上に1、3、5の数字が書かれています。
この図は、1分後には右側の図のように、数字と数字の間に新たな数字が書き足されます。このとき、新たな数字は、その両側の数字の合計になっています。上の図(右側)だと、1と3の間に4、3と5の間に8、5と1の間に6が書かれていますね。
このようにして1分ごとに数字を書き足していくとき、
(1) 4分後、円周上にある数字の合計はいくつになるでしょうか。
(2) 7分後、円周上にある数字の中で最大のものはいくつでしょうか。 |
ヒント:規則性に着目? 参考図1 参考図2 解答のページへ
|
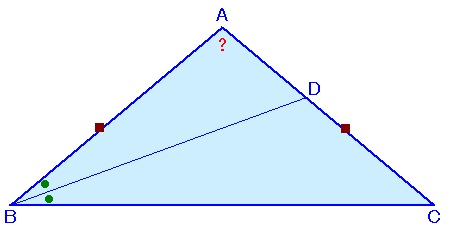
上の図は、AB=ACの二等辺三角形ABCを表しています。
いま、∠Bの二等分線をひき、辺ACとの交点をDとします。
すると、BD+AD=BCとなりました。
このとき、
(1) ∠DBCの大きさ(図中の●の大きさ)を求めてください。
(2) ∠BACの大きさ(図中の?の大きさ)を求めてください。 |
ヒント:相似に着目? 参考図1 参考図2 参考図3 解答のページへ

|
上の図のように、正方形のマス目が横に8つ並べられています。
-
まず、この8つのマス目のどれかに数字の1を記入します。
-
次に、数字の2を、1が記入されたマス目の隣(左右どちらか)に記入します。
-
次に、数字の3を、1または2のどちらかの隣に記入します。
-
4〜8の数字も順に同様に、数字がかかれたマス目の隣に記入するようにします。
このようにしたときできる数字の並び方は何通り考えられますか。
|
ヒント:次の数字を左右のどちらに? 参考図1 参考図2 参考図3 参考図4
参考図5 解答のページへ
 |
|
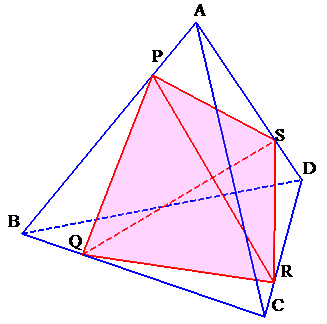
左図のような、体積が320cm3の正四面体ABCDがあります。
いま、点Pを辺AB上に、点Qを辺BC上に、点Rを辺CD上に、点Sを辺DA上に、AP:PB=BQ:QC=CR:RD=DS:SA=1:3となるようにとります。
このとき、四面体PQRSの体積は何cm3でしょうか。
|
ヒント:切り取り、立方体に内接? 参考図1 参考図2
解答のページへ |
|
球を10個の平面で切断したとき、表面は最大何個の破片に分かれるでしょうか。
|
ヒント:漸化式で考えると? 参考図1 参考図2
解答のページへ






![]()
