第400問、第399問、第398問、第397問、第396問、第395問、第394問、第393問、第392問、第391問
第400問
|
|
|
|
|
|
|
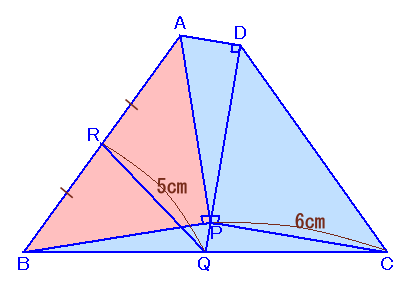 |
左図のような四角形ABCDがあります。 この四角形の内部に点Pをとったところ、△APB、△DPCはともに∠P=90度の直角二等辺三角形になり、DP=PC=6cmとなりました。また、∠ADP=90度となったそうです。 いま、DPの延長線と辺BCの交わった点をQ、辺ABの中点をRとすると、QR=5cmとなりました。 このとき、直角二等辺三角形APBの面積を求めてください。 |
|
|
|
|
|
|
ヒント:3:4:5の直角三角形? 参考図1 参考図 2 参考図3 参考図 4 解答のページへ
第399問
|
|
|
|
|
|
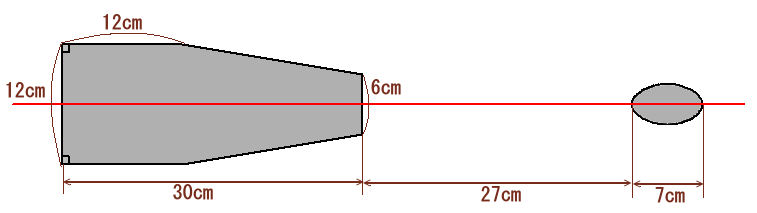
画用紙の上に立方体とボールを置いて、ある位置に豆電球を点けたところ、立方体とボールによる影が図のようになりました。(2つの影はともに赤い直線について線対称です) このとき、ボールの半径は何cmでしょうか。 |
|
|
|
|
|
第398問
|
|
|
|
|
|
ヒマ人のマサルさんが、9を2004回掛け算したところ、1913ケタの数になったそうです。 では、9を1回〜2004回掛け算してできる数のうち、先頭の数字が9である数はいくつあるでしょうか。 |
|
|
|
|
|
ヒント:9を掛けたときの結果、先頭数字が9になるとき桁上がりは? 参考図1 解答のページへ
第397問
|
|
|
|
|
|
マサルさんは、1g、4g、アg、イgの4種類の重りをそれぞれ1個ずつ持っています。(ただし、ア<イとします)
これらの重りと天秤を使うと、ウgまでの重さを1g単位で全て量ることができるそうです。ただし、重りは天秤の両 このとき、ウが最も大きくなるように、ア、イ、ウを求めて答えてください。 |
|
|
|
|
|
ヒント:重りを1個増やすごと量ることのできる重さはどうなるでしょう? 参考図1 解答のページへ
第396問
|
|
|
|
|
|
|
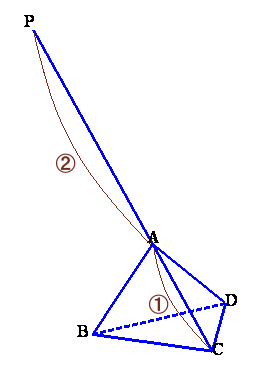 |
左図のような三角錐ABCDで、Pは辺CAをA側に3倍に伸ばした点です。 同様に、
とします。 このとき、三角錐PQRSの体積は、三角錐ABCDの体積の何倍でしょうか。 |
|
|
|
|
|
|
ヒント:いくつかの三角錐に分割すると? 参考図1 参考図 2 解答のページへ
第395問
|
|
|
|
|
|
|
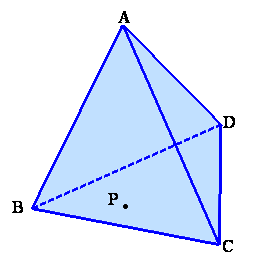 |
左図のような三角錐ABCDがあり、面BCDの内部に点Pがあります。 点Pを通り、面ACDに平行な面でこの三角錐を切断すると、頂点Bを含むほうの立体の体積は、三角錐ABCDの体積の8分の1倍になります。 また、点Pを通り、面ABDに平行な面でこの三角錐を切断すると、頂点Cを含むほうの立体の体積は、三角錐ABCDの体積の27分の8倍になります。 では、点Pを通り、面ABCに平行な面でこの三角錐を切断するとき、頂点Dを含むほうの立体の体積は、三角錐ABCDの体積の何倍でしょうか。 |
|
|
|
|
|
|
ヒント:体積の相似比=辺の相似比の3乗? 参考図1 参考図 2 解答のページへ
第394問
|
|
|
|
|
|
|
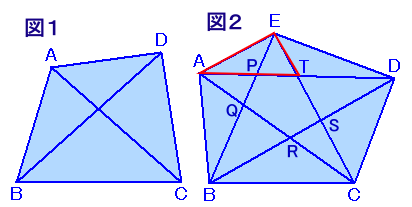 |
図1のように、凸型四角形に対角線を全て引くとき、もとの四角形の頂点を2個含む三角形は4個できますね。 では、凸型7角形に対角線を全て引くとき、もとの7角形の頂点をちょうど2個含む三角形は何個できるでしょうか。 ただし、例えば凸型5角形の場合(図2参照)、頂点Aと頂点Eを含む三角形には、図の△ATEのようなものも含むものとします。(ちなみに頂点Aと頂点Eを含む三角形は、△APE、△ATE、△AQEの3つですね。) |
|
|
|
|
|
|
ヒント:7角形の内部にある2辺を延長すると? 参考図1 参考図 2 解答のページへ
第393問
|
|
|
|
|
|
A、Bの2つの容器に濃度の異なる食塩水が入っています。 いま、A、Bからそれぞれ500gずつの食塩水を取り出し、Aから取り出した食塩水はBに、Bから取り出した食塩水はAに入れてよくかき混ぜます。すると、Aの中の食塩水とBの中の食塩水の濃度の差がx%になりました。 また、AとBに始めと同じ量・濃度の食塩水を入れ、今度はA、Bからそれぞれ620gずつの食塩水を取り出し、Aから取り出した食塩水はBに、Bから取り出した食塩水はAに入れて良くかき混ぜたところ、またまた濃度の差がx%になったそうです。 Bに始めに入っていた食塩水の量が1200gであるとすると、Aに始めに入っていた食塩水の量は何gでしょうか。 |
|
|
|
|
|
ヒント:1回目と2回目で濃度は逆転? 参考図1 解答のページへ
第392問
|
|
|
|
|
|
|
 |
一郎〜八郎までの8人兄弟が円卓で食事をすることになりました。それぞれの座席は左図のように決められています。 ある日、一郎が間違えて右隣の二郎の座席に座ってしまいました。そこで、その後に座席につく兄弟は、
ことにしました。 このとき、8人の座り方は何通り考えられるでしょうか。 |
|
|
|
|
|
|
ヒント:各自、自席より左側には座らないので? 参考図1 参考図 2 参考図3 参考図 4 解答のページへ
第391問
|
|
|
|
|
|
|
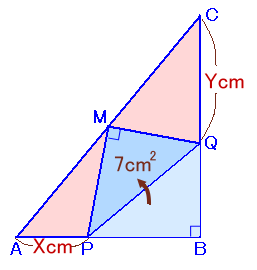 |
左図のような直角三角形ABCがあります。 いま、ACの中点Mに頂点Bが重なるように折ったところ、折り目が図の線分PQとなりました。 また、
のとき、APの長さとCQの長さの積(XとYの積)を求めてください。 |
|
|
|
|
|
|
ヒント:三角形を180度回転すると? 参考図1 参考図 2 解答のページへ