「算数にチャレンジ」にチャレンジ！(最新分)

第４３７問、第４３６問、第４３５問、第４３４問、第４３３問、第４３２問、第４３１問、第４３０問、第４２９問、第４２８問

第４３７問

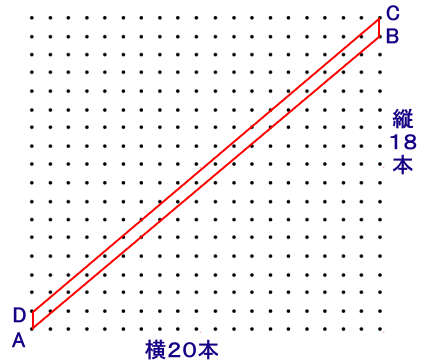左図は、ある板の上に１cm間隔で、縦１８本、横２０本の長方形になるようにクギを打ったところを表しています。

いま、この板の左下のクギＡとそのすぐ上のクギＤ、右上のクギＣとそのすぐ下のクギＢを選び、ＡＢ、ＣＤがそれぞれ一直線になるように輪ゴムをかけました。

輪ゴムの内側にあるクギを１本えらび、その１本とＡとＢを結んで三角形を作ります。このとき、できる三角形の面積は最も小さい場合で何cmでしょうか。

ヒント：三角形の面積を式で表すと？　参考図１　参考図２　参考図３　解答のページへ

第４３６問

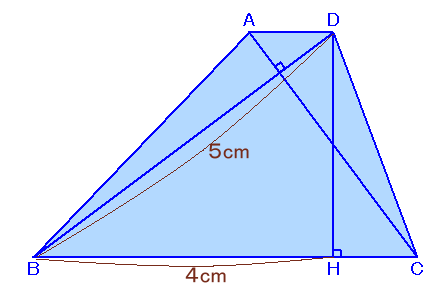左図のような台形ＡＢＣＤがあります。

いま、点Ｄから辺ＢＣに垂線ＤＨを下ろしたところ、ＢＤ＝５cmとなりました。また、対角線ＢＤと対角線ＡＣは直角に交わっており、ＢＨの長さは４cmでした。

このとき、台形ＡＢＣＤの面積を求めてください。

ヒント：AD+BCは一定？　参考図１　参考図２　参考図３　参考図４　解答のページへ

第４３５問

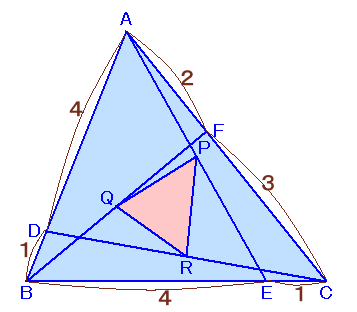左図のような、面積が１００cm²の△ＡＢＣがあります。

いま、辺ＡＢ上に点Ｄを、辺ＢＣ上に点Ｅを、辺ＣＡ上に点Ｆを、
それぞれ、ＡＤ：ＤＢ＝ＢＥ：ＥＣ＝４：１、ＣＦ：ＦＡ＝３：２と
なるようにとります。
また、線分ＡＥ、ＢＦ、ＣＤの中点（真ん中の点）をそれぞれＰ、Ｑ、Ｒとします。

このとき、△ＰＱＲの面積を求めてください。

ヒント：面積比は辺の長さの比？　参考図１　参考図２　解答のページへ

第４３４問

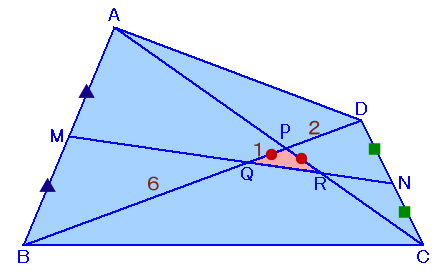左図のような四角形ＡＢＣＤがあり、ＡＢの中点をＭ、ＣＤの中点をＮとします。

いま、ＭＮと対角線ＡＣ、ＢＤの交点をそれぞれＲ、Ｑ、ＡＣとＢＤの交点をＰとします。すると、ＰＱ＝ＰＲ、ＢＱ：ＱＰ：ＰＤ＝６：１：２となりました。

このとき、四角形ＡＢＣＤの面積は、△ＰＱＲの面積の何倍か求めてください。

ヒント：高さの同じ三角形の面積比は？　参考図１　参考図２　参考図３　参考図４　参考図５　参考図６　参考図７　解答のページへ

第４３３問

ある整数を見て、１４人の人が次々にコメントを残しました。

（１人目）この整数は、２の倍数だ
（２人目）この整数は、３の倍数だ
（３人目）この整数は、４の倍数だ
　　　・
　　　・
　　　・
（１３人目）この整数は、１４の倍数だ
（１４人目）この整数は、１５の倍数だ

この１４人の中に２人だけ嘘つきが混じっていて、しかもその２人は続けてコメントしたそうです。
このとき、この整数として考えられるもののうち最小のものについて、約数の個数を求めてください。

ヒント：素因数分解？　参考図１　参考図２　　解答のページへ

第４３２問

算チャレ共和国では、次のような種類の硬貨が流通しています。

１円玉、４円玉、７円玉、１０円玉、・・・　？円玉　（１円から、３円きざみで増えています）

この国ではジュースは１本１０４円ですが、国民は上記の硬貨のうち（どのような組み合わせでもいいから）２０種類を１枚ずつ所有していれば、必ず２枚の硬貨で（ぴったり）支払うことができるので、特に不便は感じていないそうです。

では、この国で流通している硬貨の中で、最大金額のもの（上の？に当てはまる数）として考えられるもののうち、最大のものを答えてください。

ヒント：合わせて１０４円になる硬貨をグループ化？　参考図１　　解答のページへ

第４３１問

１～７の数の書かれたカードが１枚ずつ、合計７枚あります。
このカードを中の見えない袋の中に入れてよくかき混ぜ、１枚ずつ取り出して次のルールで捨てる、または箱に入れるを
決めます。

ルール：
　　取り出したカードが、それまでに取り出したカードの中で最大であれば箱の中に入れ、
　　そうでなければ捨てる。ただし、最初の１枚は箱に入れる。

このようにして７枚のカードすべてを袋から取り出したとき、捨てるカードが１枚だけであるような確からしさ（確率）を求めて下さい。

ヒント：場合分けして数え上げると？　参考図１　参考図２　参考図３　解答のページへ

第４３０問

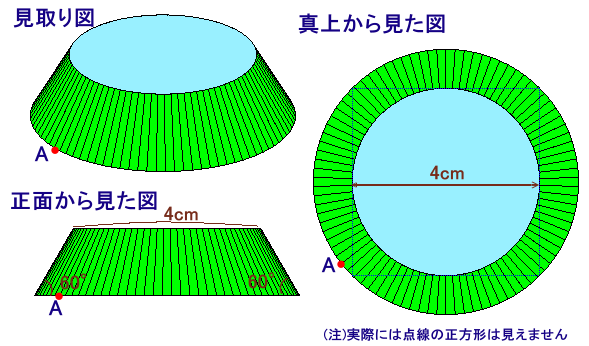左図のような、上面の円の直径が４cmである円錐台があります。

この立体を正面から見ると、底面と母線のなす角度が図のように６０°になっています。

また、この立体を真上から見ると、同心円（中心が同じで半径が異なる円）が２つ見えることになりますが、小さいほうの円がぴったり収まるような正方形は、大きいほうの円にぴったり収まるようになっています。

いま、この円錐台の下面の円の円周上にある点Ａをとります。では、点Ａからこの円錐台の側面を通って周りを１周して点Ａに帰ってくるような道のりの最短距離を求めてください。

ヒント：展開図で考えると？　参考図１　参考図２　解答のページへ

第４２９問

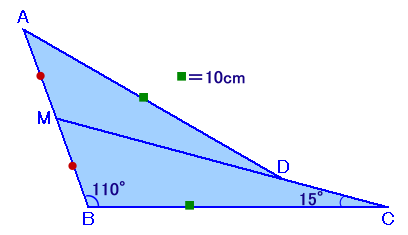左図のような、ＢＣ＝１０cm、∠ＢＣＭ＝１５度、∠ＭＢＣ＝１１０度の△ＭＢＣがあります。

いま、辺ＢＭの延長上に、ＡＭ＝ＢＭとなるような点Ａをとります。また、辺ＭＣ上に点Ｄをとったところ、ＡＤ＝１０cmとなりました。

このとき、この図形全体の面積（四角形ＡＢＣＤの面積）を求めてください。

ヒント：回転or移動？　参考図１　参考図２　参考図３　解答のページへ

第４２８問

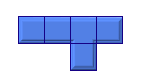左図は、一辺の長さが１cmの正方形を５つ組み合わせて作った部品を表しています。

この部品を隙間も重なりもなく組み合わせて長方形を作ることにします。

できる長方形のうち、もっとも部品の数が少なくてすむものは、縦の長さと横の長さの合計が何cmのものでしょうか。

ヒント：隅から考える？　参考図１　解答のページへ

「算数にチャレンジ」にチャレンジ！最新分