このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
122回、121回、120回、119回、118回、117回、116回、115回、 114回、113回
第122回:
| 整数を入れると、次のような動作をする装置があります。 入ってきた整数の各位の数の和を求める。これを、整数が1ケタになるまで繰り返す。
|
ヒント: 1327を9で割ると、1327=147×9+4から4が余ります。13も9で割ると、余りが4ですね。
解答のページへ:
第121回:
|
ヒント: すれ違った地点とB地点間を2人が要した時間は? 参考図 解答のページへ: |
第120回:
|
ヒント1: バスのすれ違う速度は、運行速度の何倍でしょうか? 参考図 解答のページへ: |
第119回:
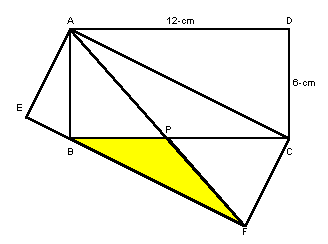 |
ヒント1: △AEB、△CBFは△ABCに相似ですね 参考図 解答のページへ: |
第118回:
| 歩幅および歩を進めるペースがそれぞれ違う、マサル君、トモエさん、ツヨシ君の3人が公園の入口にいます。3人はそれぞれ一定の速度で公園を横切って、出口に向かうことにしました。 まず、マサル君とトモエさんが20歩ずつすすみました。そして、3人同時に“出発”したところ、トモエさんは“出発”後40歩進んだところでマサル君に追いつかれました。また、ツヨシ君は“出発”後100歩進んだところでトモエさんに追いつき、その後50歩進んだところでマサル君と同時に出口に到着したそうです。また、トモエさんはツヨシ君に追い抜かれてから40歩で出口に到着したそうです。 (1)3人の歩幅の比をマサル:トモエ:ツヨシの順で最も簡単な整数で答えてください。 (例:7:8:9) (2)公園の入口から出口までの距離は90mであったそうです。マサルさんの歩幅は何cmでしょうか。 |
ヒント1: 3人が進む様子を線分で表して考え見て下さい? 参考図
解答のページへ:
第117回:
| 円のまわりに、1〜200までの番号の書かれたボールを右周りに小さい順に並べていきます。 このボールを1のボールから右周りに1つおきに取っていきます。円を一周してしまった後もボールがなくなるまでこの作業を続けます。 このとき、最後に取ることになるボールは何番のボールでしょうか。 |
ヒント1: 最初の数回を考えて見て下さい? 参考図
ヒント2: 一般的に考えるとどうでしょうか? 参考図
解答のページへ:
第116回:
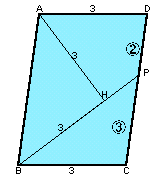 |
|
ヒント1: ADとBPを延長して交わる点をQとすると?(相似な三角形に着目) 参考図
解答のページへ:
第115回:
| 何人かの子どもたちに「マサルさんブロマイド」を配ろうと企画しました。 とりあえず1人あたりn枚ずつ配るつもりで、ちょっと多めに650枚のブロマイドを持参しました。 が、集まった子どもの人数が予定よりも20人多かったので、1人当たりに配る枚数を9枚減らしましたが、それでもあと167枚のブロマイドが必要でした。 (1) はじめに予想していた子どもの人数は何人でしょうか。 (2) nにあてはまる数はいくつでしょうか。 |
ヒント1:実際に配った枚数=実際人数×実際枚数なので、因数を考えてみると?(素因数分解)
解答のページへ:
第114回:
| 16人のメンバーが、A地点から30km離れたT地点に行くことになりました。 ところが16人には、4人乗りの乗用車が1台あるだけです。そこで、1人が運転手となって、残りの15人を3人ずつ順番に乗せて運ぶことになりました。 まず、3人(運転手を入れると4人)を乗せた車がA地点を出発します。同時に、残りの12人は歩いてT地点に向かって出発します。車はT地点に着く手前d1kmの地点で3人を降ろし、A地点方面に引き返します。降りた3人はT地点に向かって歩き始めます。 次に、引き返してきた車は、途中まで歩いてきた12人に出会うと、その中の3人を乗せて再びT地点に向かいます。もちろん、残りの9人はそのまま歩いてT地点に向かいます。車は、先に歩いている3人に追いつくと、その地点で乗っていた3人を降ろし、またまたA地点方面に引き返します。降りた3人は、歩いてきた3人と一緒にT地点に向かいます。 これを繰り返したところ、最後の3人を乗せた車が歩いている12人に追いついた地点がちょうど目的地のT地点であったそうです。 乗用車の速さは毎時60km、歩く速さは毎時4kmです。 (1) d1は、何kmでしょうか? (2) 乗用車は合計で何km走ったでしょう? |
ヒント1:歩き組がA地点から歩いて、自動車が戻ってくるまでに歩く距離と、その間自動車が進む距離の比は? 参考図
解答のページへ:
第113回:
問題:
|
ヒント1:三角形の相似で考えてみたら? 参考図
解答のページへ: