このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
132回、131回、130回、129回、128回、127回、126回、125回、124回、123回
第132回:
| マサル君はAからBまで毎時6Kmで、トモエさんはBからAへ毎時4kmで同時に出発しました。 マサル君はBに着くと15分間休んで再びAに向かって出発しました。トモエさんはAに着くとすぐにBへ引き返しました。また、2人が出会った地点は1回目と2回目で1.2Km離れていました。 さて、AB間の距離は何Kmでしょうか? |
ヒント:ダイアグラムで考えてみましょう。 参考図 解答のページへ
第131回:
 |
|
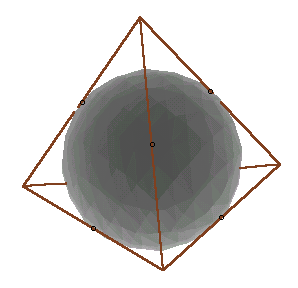
ヒント:球に外接する立方体を考えてみましょう。 参考図 解答のページへ
第130回:
 |
|
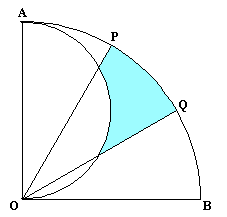
ヒント:半円AOと扇形OPQの重なる部分の面積がわかれば・・・ 参考図 解答のページへ
第129回:
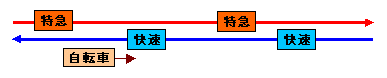
| 特急と快速がそれぞれ一定の間隔で走っている線路があります。 この線路沿いに、マサル君が自転車に乗って走ったところ、19分ごとに快速とすれちがい、また特急には38分ごとに追い抜かれました。 また、快速に乗っていたトモエさんは、特急と16分ごとにすれ違ったそうです。 では、特急に乗っていたツヨシ君は、何分ごとに快速とすれ違ったでしょうか。 |
ヒント:特急、快速およびマサル君の自転車の運行ダイアグラムを考えてみましょう 参考図 解答のページへ:
第128回:
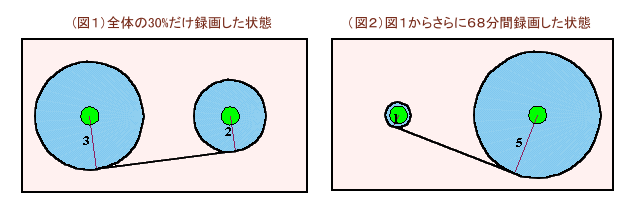
| ビデオテープがあります。 このビデオテープは、初めの状態では左側の芯にすべてのテープが巻かれており、右側の芯には巻かれていません。録画を行うと、右側のテープが左側のテープを徐々に巻き取っていきます。 このビデオテープに、録画可能時間の30%分だけ録画したところ、上の図1のように左円の半径:右円の半径=3:2になりました。 また、その後68分間録画してテープを見ると、上の図2のように、左円の半径:右円の半径=1:5になりました。 では、このビデオテープの録画可能時間は何分でしょうか? (注1)芯の半径は左右同じです。 |
ヒント:テープの長さは円の面積に比例する 参考図1、参考図2
解答のページへ:
第127回:
| 4桁の整数が2つあります。1●▲3と3●▲7です。 この2つの整数の最大公約数ができるだけ大きくなるように、●、▲を決めて下さい。 |
ヒント:2つの整数の差を考えてみましょう。 解答のページへ:
第126回:
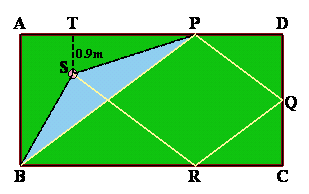 |
|
ヒント: 玉が反射するとき、反射角は等しい 参考図
解答のページへ:
第125回:
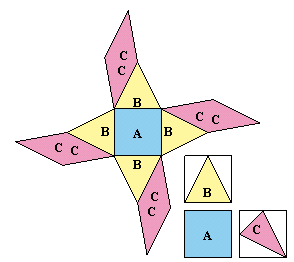 |
|
ヒント: どんな立体になるでしょう 参考図
解答のページへ:
第124回:
| 色の違う10個の箱と、見分けのつかない3つのボールがあります。 このボールを10個の箱に入れるとき、入れ方は何通りあるでしょうか? ただし、1つの箱に何個ボールを入れても構いません。 |
ヒント: 3個のボールと9個の仕切りを考えましょう 参考図
解答のページへ:
第123回:
(図1)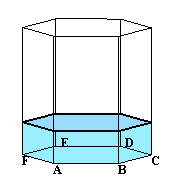 |
(図2)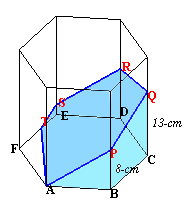 |
| (図1)のような正六角形ABCDEFを底面とする角柱の容器に水が入っています。
この容器を少し傾けたところ、(図2)のような状態になり、CQ=13cm、BP=8cmでした。(注:図2では、元の位置へ戻しています。) では、(図1)の状態のとき、水の高さは底面から何cmあったでしょうか。? |
ヒント: 水面APQRSTの延長へFから下ろした垂線の足をUとすると、どうなるでしょう? 参考図
解答のページへ: