このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
142回、141回、140回、139回、138回、137回、136回、135回、134回、133回
第142回:
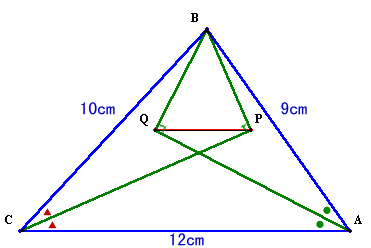 |
|
第141回:
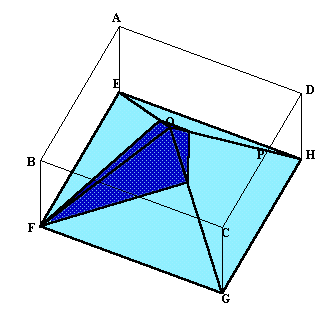 |
|
第140回:
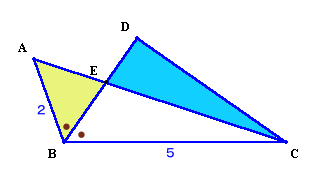 |
ヒント:BAとCDを延長してみましょう。? |
第139回:
| 9A22B8CD43は、73でも137でも割りきれる10ケタの整数です。 このとき、A、B、C、Dにあてはまる数を求めてください。 |
ヒント:73と137は互いに素ですから、73×137=10001でも割り切れる? 解答のページへ
第138回:
| まず、ある11ケタの整数を考えます。 ここで、12ケタの整数でそのうちの1つの数字を取り除くと、先ほど考えた11ケタの整数になるよ うなものを作ります。 例えば、11ケタの整数23743557911を初めに考えたとすると、12ケタの整数237435579311ならば、 百の位の数3を取り除けば、元の11ケタの整数23743557911になりますね。 では、このような12ケタの整数はいくつあるでしょうか。 |
ヒント:11ケタの整数に対し、一桁の数字を付け加えられる場所は何カ所あるでしょうか?
解答のページへ
第137回:
| A、B、C、Dの4つの箱があります。これらの箱の中には、整数の書かれたカードが何枚かずつ入っていて、次のような規則性があります。 ・A、Bの箱からカードを1枚ずつ取り出すと、その和は必ず 5で割りきれる。 ・B、Cの箱からカードを1枚ずつ取り出すと、その和は必ず 7で割りきれる。 ・C、Dの箱からカードを1枚ずつ取り出すと、その和は必ず 9で割りきれる。 ・D、Aの箱からカードを1枚ずつ取り出すと、その和は必ず11で割りきれる。 マサル君がAの箱から1枚取り出してみたところ、そのカードには1が書かれていました。また、Cの箱から1枚取り出してみると、今度は29が書かれていました。 (1)ある箱からカードを取り出したところ、218と書かれていました。このカードはA〜Dのどの箱から取り出したものでしょうか。 (2)カードに書かれた整数は、3ケタ以下の整数であるとすると、Bの箱には最大で何種類のカードが入っている可能性があるでしょうか。 |
ヒント: 整数を5,7,9,11で割った余りを考えてみましょう 解答のページへ:
第136回:
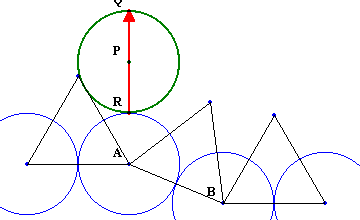 |
|
第135回:
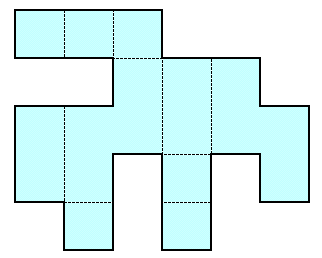 |
|
第134回:
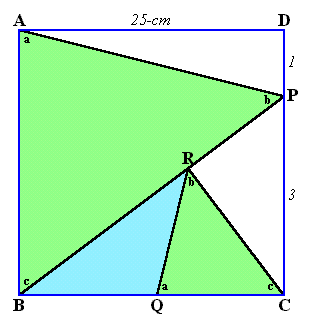 |
|
第133回:
| 忘れっぽいマサル君は、3回に1回の確からしさで訪問先にサイフを忘れてくるそうです。 いま、マサル君がトモエさん宅、ツヨシ君宅、マサヒコ君宅をこの順番で訪問して帰宅したところ、サイフを忘れてきたことに気がつきました。 では、マサル君がサイフを忘れたのがツヨシ君宅である確からしさを求めてください。 |
ヒント: どこかで忘れる確率は? 解答のページへ: