このページでは、「算数にチャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
第192問、第191問、第190問、第189問、第188問、第187問、第186問、第185問、第184問、第183問
第192問:
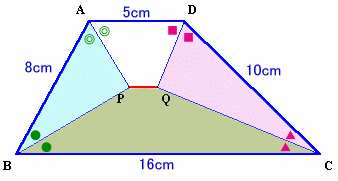 |
|
ヒント:AP、DQを延長して見ましょう。 参考図1 解答のページへ
第191問:
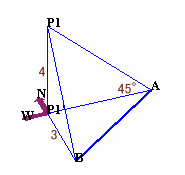 |
|
ヒント:飛行機の真下の位置を考えて見ましょう。 参考図1 参考図2 解答のページへ
第190問:
| ツヨシ君、トモエさん、マサル君の3人がある距離のかけっこをすることにしました。 3人の走る速さを分速で比べると、トモエさんはマサル君よりも分速20m速く、ツヨシ君はトモエさんよりも分速30m速いそうです。 3人が同時にスタート地点を出発したところ、第1位のツヨシ君がゴールしてから5分後にトモエさんがゴールし、トモエさんがゴールした5分後にマサル君がゴールしたそうです。 では、3人がかけっこした距離は何mでしょうか? |
ヒント:ヒストグラムで考えてみましょう 参考図1 解答のページへ
第189問:
正面から見た図 |
上から見た図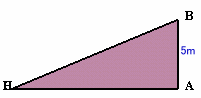 |
右から見た図 |
| 上図は、ある巨大な立体の、「上から」「正面から」「右から」見た図(注・正面および右からの図は、それぞれ一番手前の面を描いています)をそれぞれ並べたものです。この立体は、面ABC、面ACH、面ABIが平面で出来ています。 A地点からいろいろな方向に向かってまっすぐ進むとき、Bに向かうと勾配は1/5です。 また、最も坂が急になる方向だと、勾配は1/4になります。 さて、図中のCHの長さは何mでしょうか。 |
ヒント:どんな立体になるでしょうか? 参考図1 参考図2 解答のページへ
第188問:
| 2隻の舟、マサル号とトモエ号があります。 マサル号はA島からB島に向かって、トモエ号はB島からA島に向かって同じ速度で進行しています。(最初、両者は近づきつつあります) 2隻の舟からは、一定時間ごとにハトを相手の舟に向かって飛ばしています。 このとき、同じ時間にマサル号とトモエ号を飛び立った2羽のハトが出会う周期を測ったところ、最初7分ごとでしたが、途中からは11分ごとになったそうです。 |
ヒント:前のハトとの距離は? 参考図1 参考図2 解答のページへ
第187問:
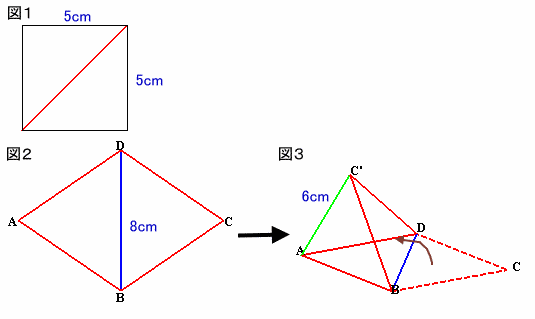
| 上の図2のような、AB、BC、CD、DAの長さがすべて、1辺5cmの正方形の対角線(図1)の長さと等しく、DB=8cmである四角形の紙があります。 この紙を、図3のようにDBを折り目にして折り曲げ、AC'(C'はCの移動先の点)=6cmになるようにしました。 このとき、三角錐C'ABDの体積を求めてください。 |
ヒント:C'ABDを2等分すれば? 参考図1 解答のページへ
第186問:
| エンピツとノートが同じ数だけあります。 エンピツはA組の13人で、ノートはB組の14人で分けました。(1人あたりの数ができるだけ多くなるように、かつみんな同じ数ずつ渡るようにします。)すると、A組の生徒が持っているエンピツの数と、B組の生徒が持っているノートの数が等しくなったそうです。 では、エンピツの総数(=ノートの数)として考えられる数は何通りあるでしょうか。 ※・・・もちろん、エンピツやノートが余っちゃうこともあります。 ※・・・どの生徒も必ず1本(1冊)はもらうものとします。 |
ヒント:正方形を1回転してできる立体の体積は? 参考図1 解答のページへ
第185問:
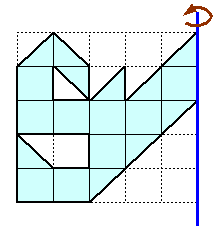 |
|
第184問:
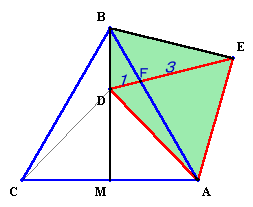 |
|
第183問:
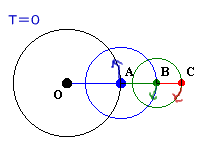 |
|
ヒント:各星間の角度差は1日あたりどれだけ開く? 参考図1 参考図2 解答のページへ
[Next]