このページでは、「もうひとつの算数チャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
62問、61問、60問、59問、58問、57問、56問、55問、54問、53問
第62問:
| 5台の自動車でレースをしました。(スタート地点は同じではありません) スタートから10秒後には1,2,3,4,5号車の順番で20mおきに等間隔でした。 スタートから100秒後には、2,5,3,1,4号車の順番で30mおきに等間隔でした。 実は、この間にも5台が等間隔に並んだときがありました。それは、スタートから何秒後のことでしょうか? |
ヒント: ダイアグラムで考えてみましょう。 参考図1 参考図2 解答のページへ
第61問:
| この分数の式が成り立つようにしたいと思います。 (1)これを成り立たせる○と□の組み合わせは何通りありますか? (2)分数を実際に作ったとき、○と□に使う数字を全て答えて下さい。 |
ヒント: 分数式を変形してみましょう。 参考図 解答のページへ
第60問:
| 数Km離れたA,B間をTORAさんとマサル君が繰り返し往復しています。TORAさんはAを、マサル君はBを同時に出発したところ、1回目にすれ違ったのは1時間後、2回目にすれ違ったのはABの中間点、3回目にすれ違ったのはAから3Kmの場所でした。 TORAさんのほうがマサル君より早く走れるとして、 |
ヒント:
ダイアグラムで考えてみましょう? 参考図 解答のページへ
第59問:
図1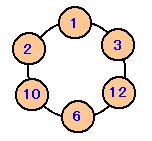 |
図2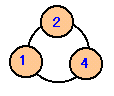 |
| 正の整数を6個選んで図1のように円周上に並べます。この6個の整数から連続したいくつかの整数を選んで、その和を計算します。最初に整数を上手に選んで、計算した和が1、2、・・と順番にできるだけ多くの連続した整数となるようにしたいと思います。 さて、最高いくつまでの連続整数を作ることができるでしょうか? (整数が3個の場合は、図2のように7が最高です。) |
ヒント:
連続した整数の並べ方がいくつあるかまず数えてみましょう? 参考図 解答のページへ
第58問:
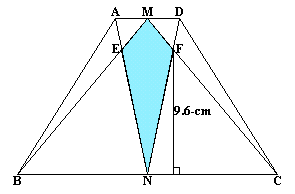
| 上図は、AD=5cmの等脚台形にいくつかの線を加えたもので、M、Nは、それぞれAD、BCの中点です。 △FNCの高さが9.6cmのとき、四角形ENFMの面積はいくらでしょうか? |
ヒント:
左右対称ですから2つの三角形に分割してみましょう? 参考図 解答のページへ
第57問:
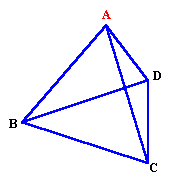 |
|
ヒント:
移動できる条件を考えて漸化式をつくってみましょう? 参考図 解答のページへ
第56問:
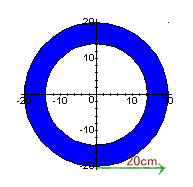 |
|
ヒント:
板が通過する部分はどんな形? 参考図
解答のページへ
第55問:
| 全校生徒1089人の学校で委員を3人選ぶ選挙をしました。 立候補したのは、A,B,C,D,E君とFさんの6人です。 開票の途中経過では、A:225,B:196,C:169,D:144,E君:121およびFさん:100票でした。 Fさんは、最低あと何票獲得すれば必ず当選するといえるでしょうか? |
ヒント:
平均より多ければ最下位にはならない? 参考図
解答のページへ
第54問:
| 1、3、9、27、81・・・のように1とそれに3を何回か掛けてできる数字を書いたカードが1枚ずつあります。 このカードの中から好きな枚数だけとりだしたとき、その合計として作ることのできない3桁の整数は全部で何個あるでしょうか? |
第53問:
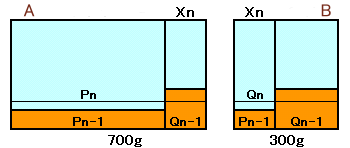
| 5%の食塩水Aが700g、10%の食塩水Bが300gあります。 まず、それぞれの食塩水から10gずつをはかりとり、AからはBへ、BからはAへと、同時に入れ替えます。 次は、20gずつ取り出して入れ替えます。3回目は30gずつ、4回目は40gずつ・・・というように、入れ替える食塩水の量を10gずつ増やしていくと、何回目の作業で2つの食塩水の濃さが等しくなるでしょうか? |
[Next]