このページでは、「もうひとつの算数チャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
52問、51問、50問、49問、48問、47問、46問、45問、44問、43問
第52問:
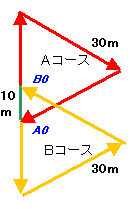 |
|
ヒント:
上記問題図をよく見ると? 参考図
第51問:
5人の人が3桁のある整数について話し合っています。
ところが、5人とも発言の一方は正しく、もう一方は誤りのようです。では、この3桁の整数とは? |
ヒント:
求める整数に1を加えると、上記条件は? 参考図
第50問:
| (1)何人かの人から千円札の寄付を募ります。1人目は、1枚か2枚か3枚かのいづれかの枚数だけ寄付してくれました。2人目以降の人は、前の人より多くはくれませんでした。この結果、寄付は千円札で30枚集まりました。さて、このような寄付の集め方は何通りでしょうか? (2)集まった30枚の千円札を、成績優秀者3名に賞金として贈ることにしました。勿論、2位の人の賞金は、1位の人より多くはなく、3位の人も2位の人より多くはありません。このような配分の仕方は何通りでしょうか? |
ヒント:
(1)3枚寄付した人の人数を固定したとき、2枚寄付した人の人数、1枚寄付した人の人数はどうなるでしょうか? 参考図
第49問:
第48問:
上図のような双六で、今93コマ目にいます。 さて、あと3回以内にゴールするようなサイコロの目の出方は何通りあるでしょうか?
ヒント:
2回サイコロを振ったとき、どのコマにいるでしょうか? 参考図
第47問:
第46問:
52枚のカードがあります。このうち、適当な枚数のカードを使って2人でゲームをします。
互いにカードを取っていき、最後にカードを取る番になったほうが負けです。
ただし、1度に取ることができるカード枚数は、1,3,4枚のいずれかです。さて、このゲームでは、最初のカード枚数によって、先手必勝か後手必勝かが決まってしまいます。52枚以内で、先手必勝になるカード枚数は、いくとおりあるでしょうか。
ヒント1:
枚数が、1から7のときを考えてみましょう。 参考図
第45問:
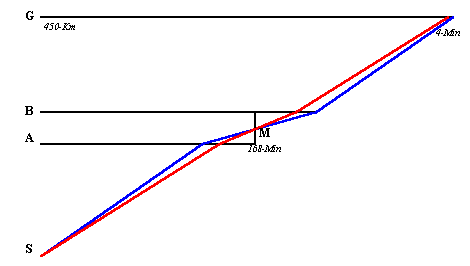
S地点からAインターまでは高速道路、AインターからBインターまでは一般道路、BインターからG地点までは高速道路で、距離の合計は450Kmです。 1号車と2号車が同時に出発後、すぐ高速道路に乗り、それぞれ時速90Km、100Kmで走ります。
Aインターでおりて、一般道路に出てからは、それぞれ減速したので、A.B間を抜けるのに1号車は60分、2号車は90分かかりました。この途中、出発後2時間48分後に1号車は2号車を追い抜きました。
Bインターから再び高速道路に入り、最初の速度で目的地まで走ったところ、1号車のほうが4分早くつきました。
さて、最初の高速道路、一般道路、2番目の高速道路の距離は、それぞれ何Kmでしょうか?
ヒント1:
SA間、AM間の所要時間の比は、どうなるでしょう? 参考図
第44問:
和が20になる整数のグループを作ります。例えば、[1,19]や[2,3,4,5,6]などで、個数に制限はありません。 さてここで、グループの整数の最小公倍数をできるだけ大きくしたいと思います。最大でいくらの大きさにできるでしょうか?
ヒント1:
和が一定の正数の積が最大になるのは、どんなとき?。 参考問題
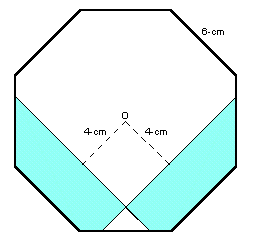
第43問:
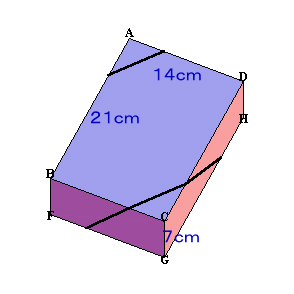
2つのコップに水が入っています。今、量の多いほうからその半分を少ないほうに移します。 この作業を繰り返し行うと、2つのコップの水の量の差が21cm3になり、さらにもう一度作業を行うと20cm3になりました。
- 2つのコップに入っている水の量は、合わせて何cm3?
- 差が20cm3になるまでは、最高で何回の作業を行ったでしょうか?
ヒント1:
一回作業を行うと、水量の差はどうなるかな? 分かったら、作業前の状態を次々と考えてみよう。 参考図
[Next]