このページでは、「もうひとつの算数チャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
82問、81問、80問、79問、78問、77問、76問、75問、74問、73問
第82問:
| ある製品を?個作って欲しいという注文にW、X、Yの3人が共同で働いて仕上げます。 Wは1個/日で3日働き1日休みます。 Xは2個/日で2日働き1日休みます。 Yは3個/日で1日働き1日休みます。 さて、注文の個数が出来上がったとき、WはXより11日多く働き、XはYより24日多く働いていました。 |
ヒント:3人働くパターンの周期を考えてみましょう。 参考図 解答のページ
第81問:
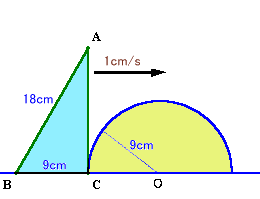 |
|
第80問:
| 各位の数字が全て異なる5桁の整数を思い浮かべてもらい、その数字を当てるゲームをしています。 当てる側が言った数字と思い浮かべた数字を比較して、数字の場所と値が合っていれば○、場所は異なるが使っている数字が含まれていれば△とし、○と△の個数を教えてもらいます。 例えば、思い浮かべた整数が「12345」で当てた側が「13579」といえば、○が1個、△が2個となります。 さて、TORAさんがゆたか君の思い浮かべた整数を当てようとしています。 TORAさんは、次の1回でゆたか君の思い浮かべた整数を見事当てることが出来るでしょうか? |
ヒント: ゆたか君が思い浮かべた整数に出てくる数字をまず確定させましょう。
0から9までの数字がそれぞれ何回ずつ出てくるかに注目して見て下さい。
解答のページへ
第79問:
 |
|
ヒント: 4つの合同な長方形に分割してみては? 参考図 解答のページへ
第78問:
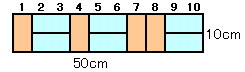 |
|
ヒント: 箱の横の長さに関する漸化式を求めてみては? 参考図 解答のページへ
第77問:
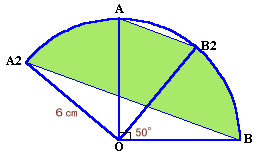 |
|
第76問:
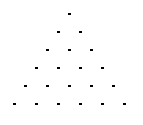 |
|
第75問:
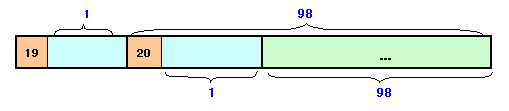
| ある小学校では、卒業生に鉛筆を配ることにしました。 1人目には19本と残りの1/99を渡し、2人目には20本と残りの1/99を、3人目には21本と残りの1/99を・・・というように規則正しく渡していきました。 すると、用意した鉛筆を余すことなく全員がちょうど同じ本数だけもらえたことになりました。 では、全部で用意した鉛筆の本数は何本あったのでしょうか。 |
ヒント: 各人のもらう鉛筆は、1本づつ増える部分と1本づつ減る部分からなりますね。
解答のページへ
第74問:
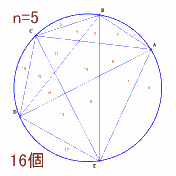 |
|
第73問:
| 毎時9kmの速度で流れる川があります。この川の下流にあるA地点から、上流のB地点まで高速艇で出発しました。 A地点を正午に出発して14分後に荷物と出会い、そのままB地点に到着したところ、先程の荷物は引き取る予定の荷物だと分かりました。 すぐに引き返したところ、ちょうどA地点まで下ったところで荷物に追いつきました。時刻は午後2時34分でした。 (1)船がB地点についたのは何時何分ですか? |
ヒント: 荷物と出会ってから上り下りに要する時間の関係は? 参考図1 解答のページへ
[Next]