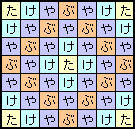「もうひとつの算数チャレンジ」にチャレンジ！#６

　このページでは、「もうひとつの算数チャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。

９２問、９１問、９０問、８９問、８８問、８７問、８６問、８５問、８４問、８３問

第９２問：

　１から順に整数番号を付けたカードが420枚あります。
まず最初、このカードを一番上が1、一番下が420になるようにきれいに重ねておきます。
そして以下の5つの操作を順に行います。
　［操作1］この束を3等分して上から2番目の束を一番上に重ねる。
　　(141,142,・・・280,1,2,・・・140,281,282,・・・420となる）
　［操作２］この束を4等分して上から3番目の束を一番上に重ねる。
　［操作３］この束を5等分して上から4番目の束を一番上に重ねる。
　［操作４］この束を6等分して上から5番目の束を一番上に重ねる。
　［操作５］この束を7等分して上から6番目の束を一番上に重ねる。

最後にできた束で、上から100番目のカードの番号は何番でしょう？

ヒント：　各操作の逆を考えてみましょう。　　参考図１　参考図２　　解答のページへ

第９１問：

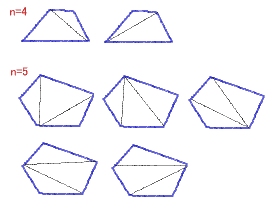　多角形を対角線で区切り、３角形に分割することを考えます。このとき対角線どうしは互いに交わらないように引きます。すると、４角形は左図のように２通り、５角形は５通りの分け方があります。
では、６角形の場合は何通りの分け方があるでしょうか？

ヒント：　６角形の１辺に注目してみましょう。
　　参考図１　参考図２　　解答のページへ

第９０問：

　長男、次男、三男の３人がじゃんけんで得点を競うゲームをしました。
　得点は、１回の勝負ごとに各自に与えられ、１人勝ちなら６点、２人勝ちならそれぞれに３点、あいこのときは３人に２点ずつが与えられます。
　計５回の勝負を行い、次のような結果になりました。

次男はぱぁを、三男はちょきを１回も出しませんでした。

長男と次男が同じ手を同時に出したのは５回の勝負のうち１回だけでした。また、長男と三男は５回中２回、次男と三男は５回中３回、同じ手を出しました。

その結果、次男の得点は計１６点、三男は計１０点になりました。

このとき、３人が出した延べ１５回の手の内訳を考えて下さい。

ヒント：　次男と三男が３回同じ手を出したのですから・・・　　参考図１　参考図２　　
　　　　　解答のページへ

第８９問：

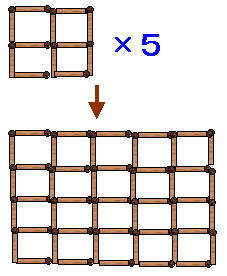１辺が１１個のマッチ棒からなる正方形を８個用意しました。
これを左図のように小さな正方形の数を変えないで並び替えて、マッチ棒を節約します。
最低何本のマッチ棒が必要でしょうか？

並び替えた形は長方形でなくてもかまいません。

ヒント：　小さな正方形と下側と右側のマッチ棒２本を対応してみてば？
　参考図　解答のページへ

第８８問：

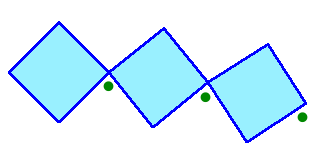左図のように、同じ大きさの正方形をたくさん用意して、１つの頂点を重ねながら並べます。
このとき、図の●印の角度が等しくなるようにします。
このようなルールで正方形を１個の大きな円を描くように並べたところ、ちょうど６０枚の正方形を並べることができたそうです。

では、●印の角度は何度でしょうか？

ヒント：　各正方形は何度ずつ偏っていますか？　参考図　解答のページへ

第８７問：

整数Ａと整数Ｂがあります。この２つはともに２桁の整数で、ＡとＢの和を計算すると２桁のゾロ目に、またＡとＢの積を計算すると３桁のゾロ目になるそうです。
このようになる２つの整数Ａ、Ｂはいくらでしょうか？

ヒント：　３桁のゾロ目は何の倍数？　　解答のページへ

第８６問：

図１
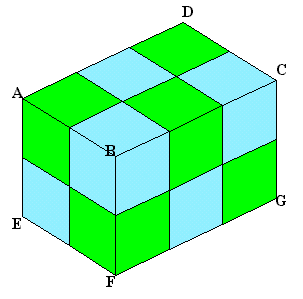
図２

１から６までの数字を書いた立方体が１２個あります。
それぞれの数字は図１のようになっていて、対面どうしの和は７になっています。
この１２個を、同じ数字が書いている面どうしを張り合わせるというルールのもとに組み立てて図２のような直方体を作ります。

出来上がった直方体の表面に書かれている３２個の数字の和ができるだけ大きくなるように組み立てた場合、その合計はいくらにすることが可能でしょうか？

ヒント：　角の数字を大きくするには？　参考図１　　解答のページへ

第８５問：

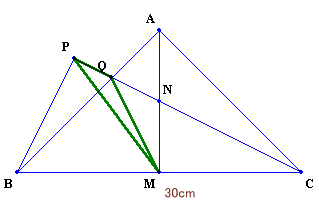左図でＡＢＣは直角２等辺三角形、ＭとＮはそれぞれＢＣ，ＡＭの中点、角ＢＰＣは９０度、ＢＣの長さは３０ｃｍになっています。
このとき、三角形ＰＱＭの面積は何ｃｍ²になりますか？

ヒント：　直角三角形の相似？
　参考図１　　解答のページへ

第８４問：

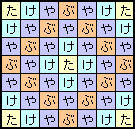左図の中に「たけやぶやけた」と読むことができる並びは、何通りありますか？
ただし、同じ場所を２度通っても構いませんが、隣り合っていないマスに跳んではいけません。
また、同じルートを逆向きに読む場合は、別個に数えて下さい。

ヒント：　最短経路？　参考図１　　解答のページへ

第８３問：

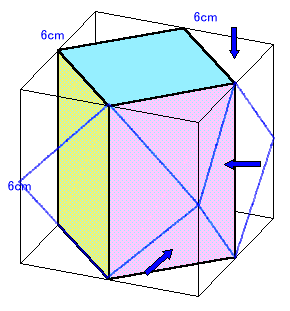
上図は、１辺が６ｃｍの立方体の上面と下面の各辺の中点を通る平面で立方体の四隅を切り落としてできた直方体です。
左右の面および前後の面からも同様にして四隅を切り落としてできる立体の体積を求めて下さい。

ヒント：　求める立体はどんな形？　参考図１　　解答のページへ

[Next]