このページでは、「もうひとつの算数チャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
102問、101問、100問、99問、98問、97問、96問、95問、94問、93問
第102問
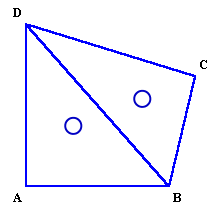 |
ヒント:三角形ABCを切りとって別のところに移してみましょう。
|
第101問:
| 碁石がn個(ただしn≧1)あります。 2人でこの碁石を交互に取っていくゲームをします。 ルールは次の通りです。
このとき、後手必勝となるのはnがいくつのときでしょうか? |
ヒント:前の人がm個取ってn個になった状態を、nが小さい順に考えてみましょう。 参考図 解答のページへ
第100問:
| A、B2つの水槽があって、Aには1999dlの水が入っていてBは空になっています。 この水槽の水を次のように操作します。
このとき、水槽Aに入っている水の量は何dlでしょうか? |
ヒント:全体の水の量を1として、初めの数回を考えてみましょう。参考図 解答のページへ
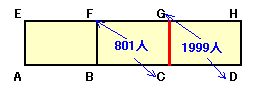
第99問:
 |
|
ヒント:AE,BF,CG,DHを通った人を考えてみましょう 解答のページへ
第98問:
図1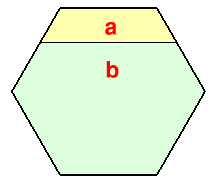 |
図2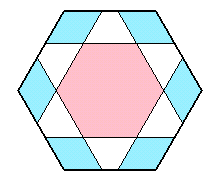 |
| 図1のように、正六角形の辺に平行な線を1本引いて、区切られた2個所の面積比がa:bとなるように分割しました。 さらに、他の5つの辺に沿っても同様な線を引いて図2のような図形を作りました。 すると、中心部分にできた小さな六角形の面積と水色の部分の面積が等しくなったそうです。 では、a:bはいくらだったでしょうか? |
ヒント:正六角形の対角線で分割すると? 参考図1 解答のページへ
第97問:
| 白石と黒石と小箱が何個かずつあります。 最初それぞれの小箱に白石と黒石の個数の比が5:9になるように石を入れていこうとしたところ、白石は3個余り、黒石は6個不足しました。 では、白石は何個あるのでしょうか? |
ヒント:白石5個、黒石9個と白石4個、黒石7個を袋に? 参考図1 参考図2 解答のページへ
第96問:
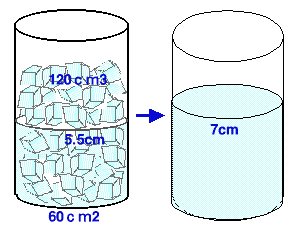 |
|
第95問:
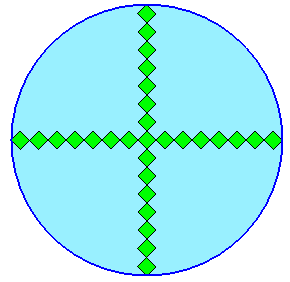 |
|
第94問:
| ある月の1日から31日まで、毎日XとYの2種類の製品を1個ずつ購入することになりました。以下は、この製品の値動きを記録したものです。 製品Xと製品Yの値段は、1日には同じでした。 この1ヶ月の間にXを購入するのに要した代金の総額は、Yと比べていくら多かったのでしょう? |
ヒント: X,Yのグラフの面積を考えてみましょう。 参考図1 解答のページへ
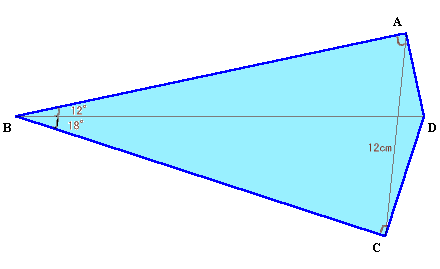
第93問:
| 上図のABCDはAとCの角度が共に90°の四角形です。 対角線ACの長さが12cmのとき、もう一方の対角線BDは何cmでしょうか? |
ヒント: ABCDの外接円を考えてみましょう。 参考図1 解答のページへ
[Next]