このページでは、「もうひとつの算数チャレンジ」にチャレンジした問題の中で、特に面白かった問題について取り上げてみたいと思います。
112問、111問、110問、109問、108問、107問、106問、105問、104問、103問
第112問:
|
某弁当屋では、毎日一定数の弁当を作って1個800円で販売しています。 では、この弁当の1個あたりの製造コストはいくらでしょう? |
ヒント: 昨日から今日で増えた利益から製造個数を求めてみましょう。 参考図 解答のページへ
第111問:
|
幅の広い下りのエスカレータがあります。A君、B君の2人が、各々のペースでこのエスカレータを9分間上り下りし続けます。このとき、A君が下る速さとB君が上る速さは、等しかったそうです。
では、2人が最後にすれ違ったのは、下から何段目の場所でしょう? |
ヒント: A君、B君の進み方をダイアグラムで考えましょう。 参考図1 解答のページへ
第110問:
図1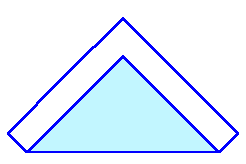 |
図2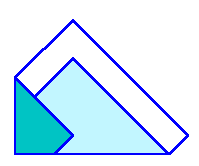 |
正方形の折り紙が1枚あります。 |
ヒント: 重なり具合を考えましょう。 参考図1 参考図2 解答のページへ
第109問:
| AチームとBチームが4戦先取の7回戦試合をすることになりました。 1回戦はAチームが勝ちました。(試合はどちらかのチームが4勝した時点で打ち切ります) では、残りの試合結果は何通りあると考えられるでしょうか? |
ヒント: Aチームの勝ち、Bチームの勝ちで場合分けしましょう。 参考図1 解答のページへ
第108問:
| ある食塩水に、99gの食塩を加えると濃度(%)が7.2ポイント上昇します。 また、99gの水を加えると濃度(%)は1.8ポイント下降します。 (1)この食塩水は何gありますか。 |
ヒント: 食塩水の変化を図示しましょう。 参考図1 解答のページへ
第107問:
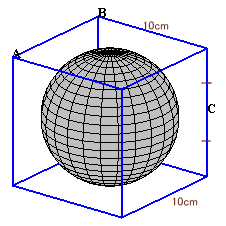 |
参考図1 参考図2 解答のページへ |
第106問:
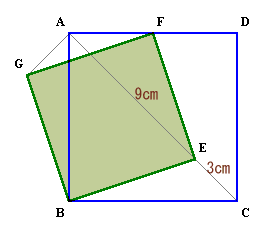 |
参考図1 参考図2 参考図3 解答のページへ |
第105問:
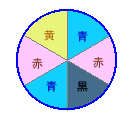 |
|
ヒント: 同じ色を使う必要が出てきます。場合分けしてみましょう。 解答のページへ
第104問:
| 1枚で1ポイントのBronzeカードがあります。 このカードを規定枚数(A枚)集めると、1枚AポイントのSilverカード1枚と交換してもらえます。 また、同様にSilverカードはB枚集めるとGoldカード1枚と、さらにGoldカードはC枚でPlatinumカード1枚と交換できます。 ゆたか君は、このカードを集めています。Bronze、Silver、Goldの3種類のカードが集まりましたが、どれも規定枚数に1枚だけ足りていません。ただ、このときのポイント数合計はちょうど1000ポイントでした。 これを知った友達が、Bronze、Silver、Goldそれぞれのカードを1枚ずつ譲ってくれました。 では、規定枚数A、B、Cはいくらだったのでしょうか? |
ヒント: 題意をA,B,Cの式で表してみましょう。 解答のページへ
第103問:
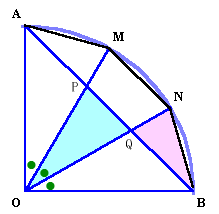 |
|
[Next]